青岛oj集训10

最重要：01背包（完全背包）

设dp[i][j]表示前i个物品装进容量为j的背包

分两种情况，要么不要（第一项），要么要（第二项）f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i])

注意，要判断j-w[i]是否为正

完全背包：

f[i][j]=max(f[i-1][j],f[i][j-w[i]]+v[i])

空间优化：

因为上一行用完就不会再用了

每次只会用到上一行的数据

所以只需要保留i-1和i这两行就行

所以考虑滚动数组

原来的数组：

f

|  |  |  |  |  i=1

|  |  |  |  |  i=2

|  |  |  |  |  i=3

……

现在的数组：

f

|  |  |  |  |   i=1,3,5,…

|  |  |  |  |   i=2,4,6,…

所以只需要把所有f数组里的"i"变成i%2就行

这种方法很多dp都可以用

那么还有一种方法可以只用一维，但是只有背包能用

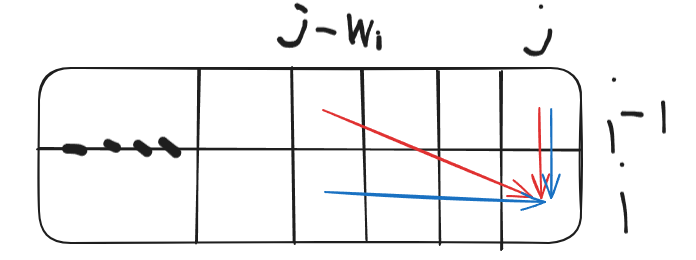
观察到01背包（红）在更新f[i][j]的时候需要f[i-1]的值还未被更新，所以想要大的更新了小的没更新，要逆序枚举

而多重背包（蓝）在更新时需要f[i-1]已经更新，所以要正序枚举

P2979

有两种情况

如果没有大奶酪，那么就是最最最最普通的完全背包

因为我们要尽可能多的奶酪被压扁

先枚举上边的大奶酪是哪一种

再把背包大小变成m*5/4-大奶酪高度

再跑完全背包

but

放上大奶酪也不一定就好

所以你要判断一下，把这种情况和最普通的完全进行比较，选最大的

1941

呵呵，绿题我能会就怪了

这是一道背包题，想不到吧

先假设这是一道简单的dp题

定义f[i][j]表示小鸟在(i,j)位置的最小步数

考虑没有柱子的情况

f[i][j]可以从f[i-1][j+y]或f[i-1][j-x]+1 , f[i-1][j-2x]+2……转移过来

如果你真这么做，那么O(nm^2)直接炸

会发现这些方程有点熟悉

f[i-1][j+y]不就是01背包吗？（-变成+了）

f[i-1][j-x]+1 , f[i-1][j-2x]+2……

不就是f[i][j-w[i]]+v[i]完全背包吗？

所以就是完全背包+01背包

柱子呢？

如果f[i][j]这个位置和柱子重合了

那么直接赋值为inf

多重背包

如果把每个都拆开成一个一个的小物品做01背包三层循环O(nms[i])太大了

那么二进制优化

会发现对于任何一个正整数n

找到2^（k-1）< n < 2^k

则n可以写成1+2+4+8+…+2^（k-2）+剩下的差

如40=1+2+4+8+16  +  9

那么一个物品就会被拆成log下取整+1个数

这样就优化多了

分组背包

首先是一堆01

给它分个组，每个组里只能选一个

P1782

呵呵，蓝题，呵呵呵呵哈哈哈

前半部分：标准的多重背包，用二进制优化不然就炸

后半部分：分组背包，枚举X

可行性背包

第0列赋值1，O(nm)

但是会发现里面存的都是0,1

所以可以用bitset优化

bool qwq[5]={1,0,1,1,1};

那么bitset也就是10111

bitset<5> qwq=10111

它可以看做一个二进制数，左边是低位，右边是高位

即11101

对其右移1位：1101

那么bitset就变成1011（所以反了）

这是直接用bool数组O(nm)

注意！！标蓝的>>变成<<

会比直接用bool快64（机器字长）倍

P5020

先将a排个序

那么a₁一定在新的货币系统中

那么就可以把所有a₁的倍数都删掉

再取最小的（假设是a2）

然后再把能用a₁和a₂都删掉直到没有

令f[i]表示i能否被新货币表示出来

若枚举到ai为0，则这个就是无法被表示的，就新加入货币系统，更新货币系统

P1537

判断：能否凑出一些弹珠为总价值的一半

多重可行性背包

但是直接跑6*2*10^4*2*10^4肯定过不了

你可以二进制优化O(6*log(n[i])*n)

当然，你可以再进行bitset优化，再快64倍O(6*log(n[i])*n/64)

注意！！！状态转移方程是w_i和v_i打反了，不然也就没啥变化了

f[i][j]的定义很重要！！

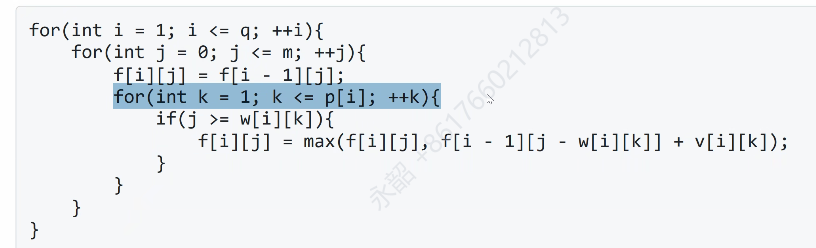
AT_abc364_e [ABC364E] Maximum Glutton

f[i][j][k]表示前i个物品，甜度为j，咸度为k，的最大菜肴

发现答案的值域很小，所以考虑把答案和甜/咸换一下