详解HarmonyOS NEXT仓颉开发语言中的全局弹窗

之前分享过仓颉开发语言中的自定义弹窗，那一次的自定义弹窗需要在对应页面先初始化再进行弹出，不是很方便。今天分享一下不依赖页面的全局弹窗。

仓颉提供了全局弹窗模块prompt_action，使用之前先将它导入：

import ohos.prompt_action.*

该模块提供了三种预设好的弹窗形式，第一种是简单的文字提示，可以设置弹窗内容，弹窗持续时间、弹窗模式等属性，使用方式如下：

PromptAction.showToast(message: '这是一个弹窗', duration: 4000, bottom: "80vp", showMode: ToastShowMode.Default)

你可以在任意页面任何地方随时调用，非常方便。看一下效果：

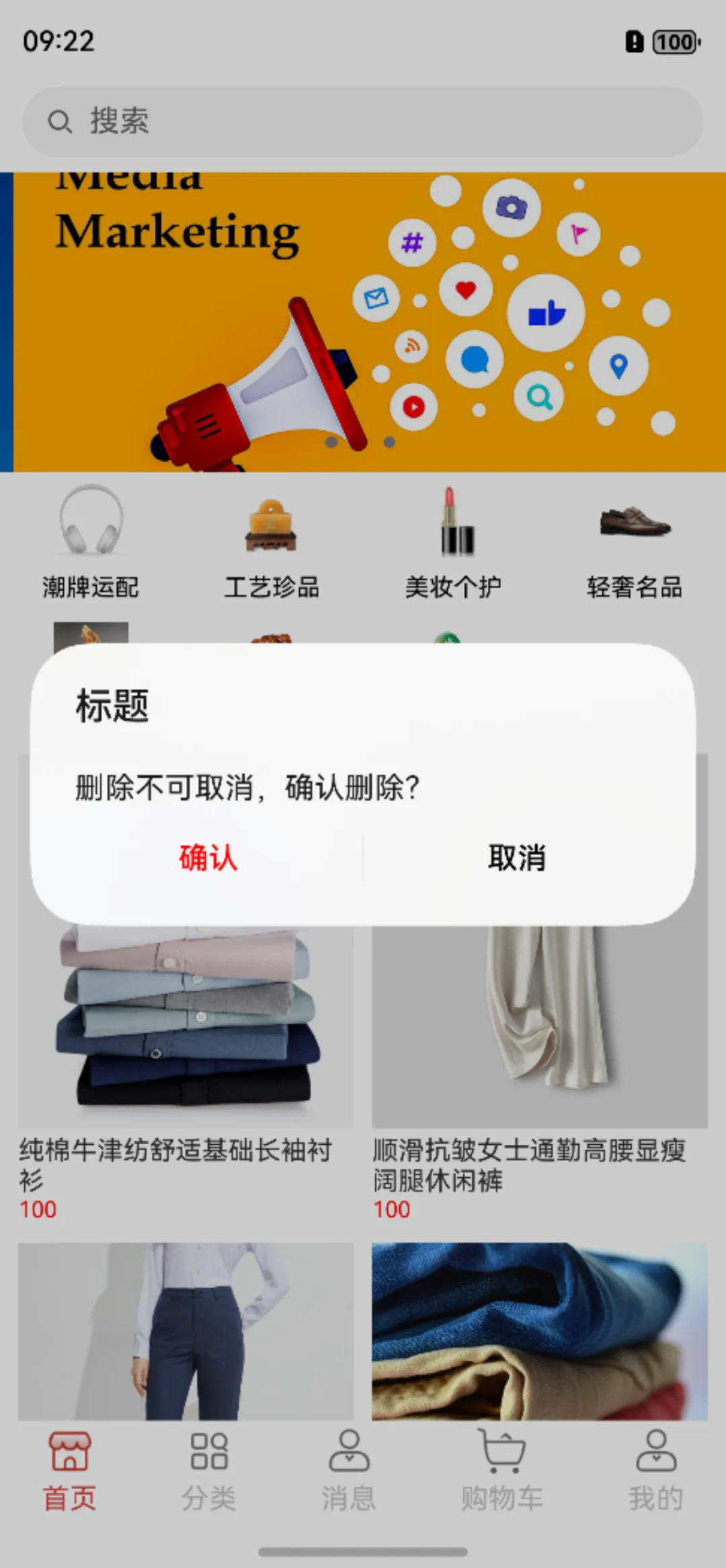
第二种是对话弹窗，内容有标题、内容和按钮的提示弹窗，比上一种弹窗内容丰富了些，适用于大多数场景，使用方式如下：

let buttons: Array<ButtonInfo> = [
  ButtonInfo("确认", Color.RED),
  ButtonInfo("取消", Color.BLACK)
]

PromptAction.showDialog(title: "标题", message: "删除不可取消，确认删除？", buttons: buttons, callback: { err: Option<AsyncError>, i: Option<Int32> =>

  })

弹窗效果图如下：

第三种是菜单弹窗，支持传入1到6个按钮，使用方式和对话框类似：

let buttons: Array<ButtonInfo> = [
  ButtonInfo("选项1", Color.BLACK),
  ButtonInfo("选项2", Color.BLACK)
]
PromptAction.showActionMenu(title: "标题", buttons: buttons, callback: { err: Option<AsyncError>, i: Option<Int32> =>

  })

效果图如下：

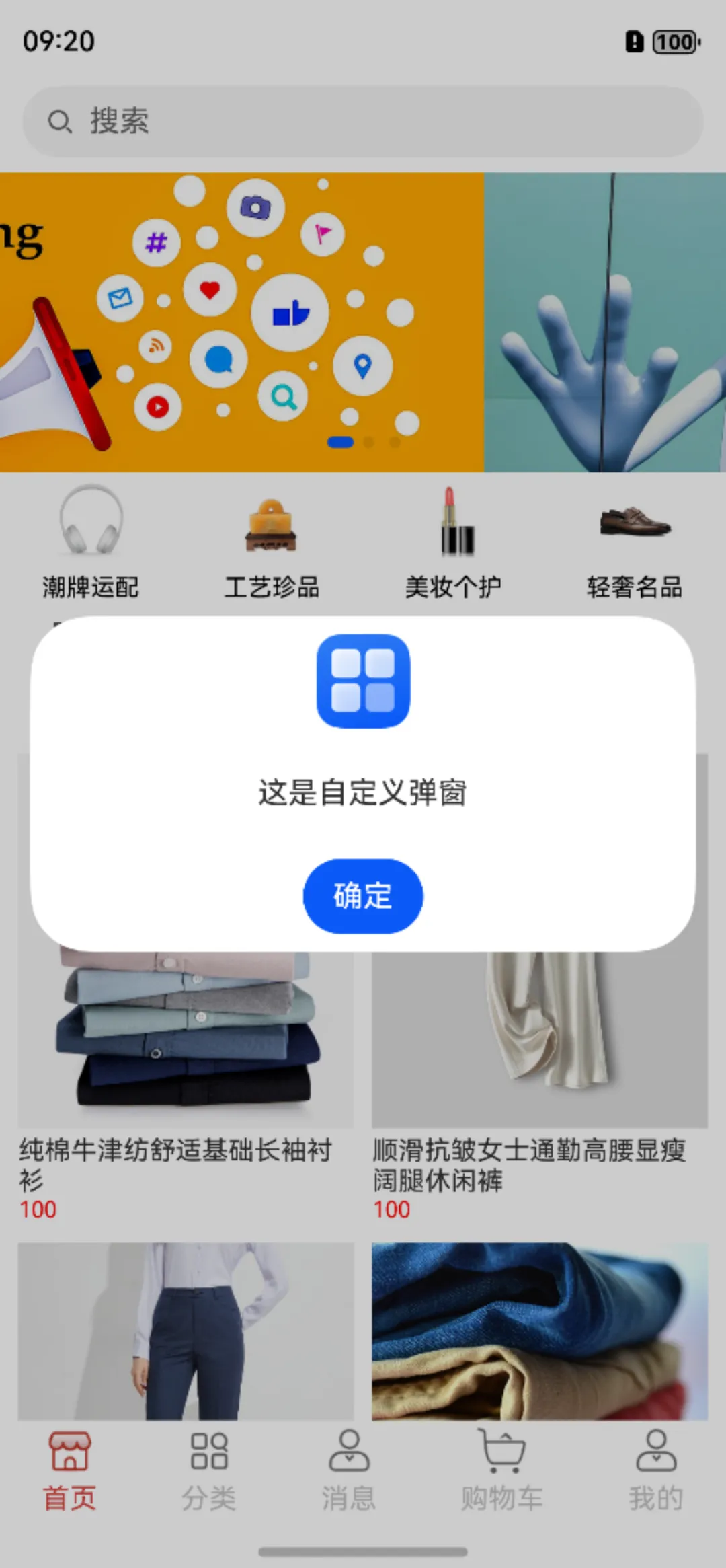
如果这三种弹窗都不能满足你的要求，PromptAction还支持设置自定义内容，它会返回弹窗的id，我们可以根据id来关闭弹窗，具体使用方式如下：

@State var customdialogId:Int32 = 0

@Builder
func CustomDialog() {
    Column(10) {
        Image(@r(app.media.startIcon))
        .width(50)
        .height(50)
        Text("这是自定义弹窗")
        .height(50.vp)
        Button("确定")
        .onClick({
            => PromptAction.closeCustomDialog(customdialogId)
        })
    }
    .margin(10.vp)
}

PromptAction.openCustomDialog(CustomDialogOptions(builder: bind(this.CustomDialog, this)),{ id =>
            customdialogId = id
            })

以上就是仓颉语言中全局弹窗的相关内容，感谢阅读。##HarmonyOS语言##仓颉##购物#