[题解]AtCoder Beginner Contest 407(ABC407) A~F

A - Approximation

使用<cmath>中的round()函数实现四舍五入。

时间复杂度\(O(1)\)。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int a,b;
signed main(){
	cin>>a>>b;
	cout<<round(1.0*a/b);
	return 0;
}

B - P(X or Y)

枚举两次的点数，统计满足条件的个数，最后求出比例即可。

时间复杂度\(O(|\Sigma|^2)\)，其中\(|\Sigma|=6\)。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int x,y,cnt;
signed main(){
	cin>>x>>y;
	for(int i=1;i<=6;i++){
		for(int j=1;j<=6;j++){
			if(i+j>=x||abs(i-j)>=y) cnt++;
		}
	}
	cout<<fixed<<setprecision(18)<<1.0*cnt/36<<"\n";
	return 0;
}

C - Security 2

考虑把过程倒过来，先让最后一位通过\(-1\)操作变成\(0\)，然后向前以此类推……

注意\(+1\)操作是所有数共同进行的，所以我们需要记录\(cnt\)变量表示到目前为止的\(+1\)操作个数，处理某位时，需要先对该位进行\(cnt\)次\(-1\)操作，再统计贡献。

别忘了添加\(0\)也是一次操作。

时间复杂度\(O(n)\)。

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
string s;
int n,cnt;
signed main(){
	cin>>s;
	n=s.size();
	for(int i=n-1;~i;i--){
		int v=(s[i]-'0'-cnt)%10;
		(v+=10)%=10;
		cnt+=v;
	}
	cnt+=n;
	cout<<cnt<<"\n";
	return 0;
}

D - Domino Covering XOR

DFS搜索骨牌的放置方案，从左上角开始，遇到一个空格子，那么这个格子可以有\(3\)种状态：

• 与右边的格子共用一张骨牌。
• 与下边的格子共用一张骨牌。
• 不放骨牌。

不过这样子方案数太多，因为覆盖格子集合相同的情况下，我们还在考虑骨牌的不同放置方法，然而这是冗余的。

所以用\(f[x][y][S]\)记忆化一下就可以了，其中：

• \((x,y)\)是当前正在考虑的位置。
• \(S\)是覆盖格子的集合，可以压成一个整数。

时间复杂度\(O(2^{nm}nm)\)。

点击查看代码

#include<bits/stdc++.h>
#define int long long
#define N 25
using namespace std;
int n,m,a[N][N],ans;
bitset<1<<20> f[N];
inline int toint(int x,int y){return (x-1)*m+(y-1);}
void dfs(int x,int y,int sta,int sum){
	if(y>m) y-=m,x++;
	if(x>n){ans=max(ans,sum);return;}
	if(f[toint(x,y)][sta]) return;
	f[toint(x,y)][sta]=1;
	if(!((sta>>toint(x,y))&1)){
		dfs(x,y+1,sta,sum);
		sta^=(1<<toint(x,y)),sum^=a[x][y];
		if(y<m&&!((sta>>toint(x,y+1))&1)) dfs(x,y+1,sta^(1ll<<toint(x,y+1)),sum^a[x][y+1]);
		if(x<n&&!((sta>>toint(x+1,y))&1)) dfs(x,y+1,sta^(1ll<<toint(x+1,y)),sum^a[x+1][y]);
	}else dfs(x,y+1,sta,sum);
}
signed main(){
	cin>>n>>m;
	int X=0;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>a[i][j],X^=a[i][j];
		}
	}
	dfs(1,1,0,X);
	cout<<ans<<"\n";
	return 0;
}

E - Most Valuable Parentheses

一个括号序列是合法的，当且仅当：

• 对于奇数\(i\)，长度为\(i\)的前缀至少有\(\lceil \frac{i}{2}\rceil\)个左括号。
• 左括号数量\(=\)右括号数量。

所以遍历每个元素\(i\)，如果\(i\)是奇数，就说明必须补充一个左括号。

这个左括号可以从前\(i\)个位置中还没放左括号的位置随意选择，用优先队列贪心即可。

时间复杂度\(O(Tn\log n)\)。

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
int t,n,ans;
priority_queue<int> q;
void solve(){
	cin>>n;
	for(int i=1,x;i<=2*n;i++){
		cin>>x;
		q.push(x);
		if(i&1) ans+=q.top(),q.pop();
	}
	cout<<ans<<"\n";
	ans=0;
	while(!q.empty()) q.pop();
}
signed main(){
	cin>>t;
	while(t--) solve();
	return 0;
}

F - Sums of Sliding Window Maximum

需要对\(k=1,2,\dots,n\)求解，所以思路大概有下面\(2\)种：

• 递推求解。
• 同时统计\(k\in[1,n]\)的答案。

前者没想出，后者就好考虑一些。

具体来说，对于\(a[i]\)，考虑如下问题：

• 给\(ans[1]\)的贡献是多少？
  
  —— 有多少个长度为\(1\)的区间以\(a[i]\)为最大值？
• 给\(ans[2]\)的贡献是多少？
  
  —— 有多少个长度为\(2\)的区间以\(a[i]\)为最大值？
• \(\dots\)

拿下图举个例子：

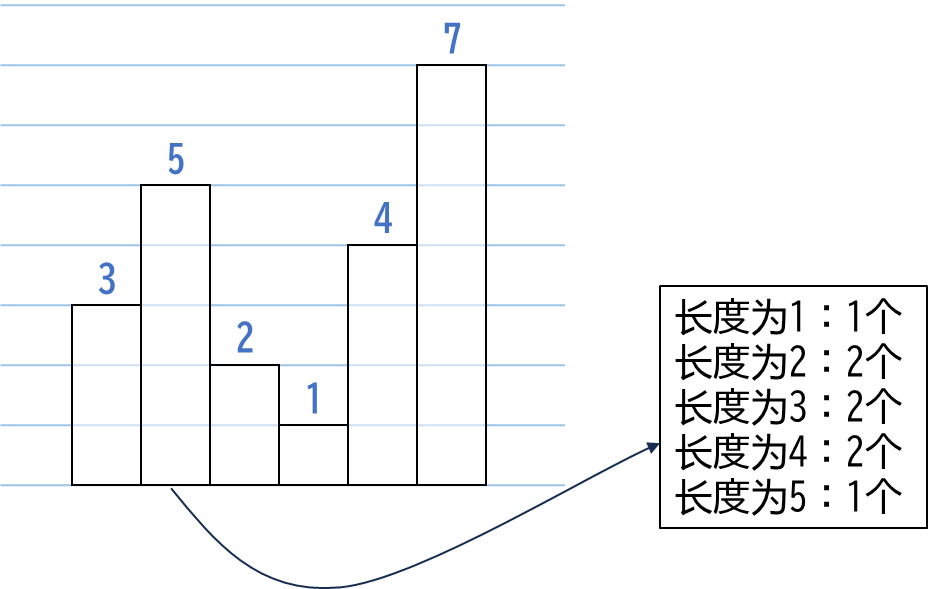
实际上通过举几个例子，不难发现，任何一个\(a[i]\)对\(ans[1],ans[2],\dots\)的贡献都可以写成形如这样的序列：

\[1,2,\dots,x-1,x,x,\dots,x,x-1,\dots,2,1
\]

（实际上还要\(\times a[i]\)再累加。）

其中：

• 序列的总长度是\(R[i]-L[i]+1\)。
  • \(R[i]\)表示最大的\(j\ge i\)使得\(\max a[(i+1)\sim j]\le a[i]\)。
  • \(L[i]\)表示最小的\(j\le i\)使得\(\max a[j\sim (i-1)]<a[i]\)。
• \(x=\min(R[i]-i,i-L[i])+1\)。

\(L,R\)的定义为什么是一个\(\le\)一个\(<\)？

• 如果都是\(<\)，则“\(a[i],a[j]\)同时为某区间的最大值”的情况会被忽略。
• 如果都是\(\le\)，则“\(a[i],a[j]\)同时为某区间的最大值”的情况会被统计\(2\)次。

这一串序列如果直接暴力累加到\(ans\)上，单次时间复杂度是\(O(n)\)的，无法接受。

但是不难发现上面序列的差分数组形如：

\[1,1,\dots,1,1,0,0,\dots,0,0,-1,-1,\dots,-1,-1
\]

再差分一下：

\[1,0,0,0,\dots,-1,0,0,0,\dots,-1,0,0,0,\dots,1
\]

所以直接修改这个双重差分数组即可。

最后对它求两次前缀和即可还原出\(ans\)数组。

---

至于怎么求\(L,R\)，一开始写的是非常笨蛋的ST表+二分。时间复杂度\(O(n\log n)\)。

实际上用单调栈即可，见第\(2\)份代码。时间复杂度\(O(n)\)。

ST表+二分

#include<bits/stdc++.h>
#define int long long
#define N 200010
using namespace std;
int n,a[N],lg[N],maxx[N][25],sum[N];
void init(){
	lg[0]=-1;
	for(int i=1;i<=n;i++) lg[i]=lg[i/2]+1,maxx[i][0]=a[i];
	for(int i=1;i<=lg[n];i++){
		for(int j=1;j+(1<<i)-1<=n;j++){
			maxx[j][i]=max(maxx[j][i-1],maxx[j+(1<<(i-1))][i-1]);
		}
	}
}
int maxr(int l,int r){
	if(r<0||l>n||l>r) return INT_MIN;
	int len=lg[r-l+1];
	return max(maxx[l][len],maxx[r-(1<<len)+1][len]);
}
int findl(int R,int x){
	int l=1,r=R;
	while(l<r){
		int mid=(l+r)>>1;
		if(maxr(mid,R-1)<=x) r=mid;
		else l=mid+1;
	}
	return l;
}
int findr(int L,int x){
	int l=L,r=n;
	while(l<r){
		int mid=(l+r+1)>>1;
		if(maxr(L+1,mid)<x) l=mid;
		else r=mid-1;
	}
	return l;
}
signed main(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	init();
	for(int i=1;i<=n;i++){
		int l=findl(i,a[i]),r=findr(i,a[i]);
		int siz=r-l+1,len=min(i-l,r-i)+1;
		sum[1]+=a[i],sum[len+1]-=a[i];
		sum[siz-len+2]-=a[i],sum[siz+2]+=a[i];
	}
	for(int i=1;i<=2;i++) for(int j=1;j<=n;j++) sum[j]+=sum[j-1];
	for(int i=1;i<=n;i++) cout<<sum[i]<<"\n";
	return 0;
}

单调栈

#include<bits/stdc++.h>
#define int long long
#define N 200010
using namespace std;
int n,a[N],st[N],top,l[N],r[N],sum[N];
signed main(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i],l[i]=1,r[i]=n;
	for(int i=1;i<=n;i++){
		while(top&&a[st[top]]<a[i]) r[st[top--]]=i-1;
		st[++top]=i;
	}
	top=0;
	for(int i=n;i;i--){
		while(top&&a[st[top]]<=a[i]) l[st[top--]]=i+1;
		st[++top]=i;
	}
	for(int i=1;i<=n;i++){
		int siz=r[i]-l[i]+1,len=min(i-l[i],r[i]-i)+1;
		sum[1]+=a[i],sum[len+1]-=a[i];
		sum[siz-len+2]-=a[i],sum[siz+2]+=a[i];
	}
	for(int i=1;i<=2;i++) for(int j=1;j<=n;j++) sum[j]+=sum[j-1];
	for(int i=1;i<=n;i++) cout<<sum[i]<<"\n";
	return 0;
}