混沌分形之逻辑斯蒂（Logistic）映射系统

前几天，有个同事看到我生成的一幅逻辑斯蒂分岔图像后，问我：“这是咪咪吗?”我回答：“淫者见淫。”好吧，这里将生成几种分岔映射图形，包括逻辑斯蒂映射系统，正弦映射系统和曼德勃罗映射系统。实际上这几种图形算不上分形，只不过它与我写的其他分形对象使用相同的基类，所以也将其列入混沌分形的范畴。

关于基类FractalEquation的定义及相关软件见：混沌与分形

（1）逻辑斯蒂映射系统

// 逻辑斯蒂映射系统
class LogisticMap : public FractalEquation
{
public:
    LogisticMap()
    {
        m_StartX = 0.0f;
        m_StartY = 0.0f;
        m_StartZ = 0.0f;

        m_ParamA = 0.0f;
        m_ParamB = 4.0f;

        m_nIterateCount = ;
    }

    void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
    {
        float R = (float)rand()/RAND_MAX;
        float k = m_ParamA + (m_ParamB - m_ParamA) * R;
        outX = R*4.0f;

        outY = (float)rand()/RAND_MAX;
        for (int i = ; i < m_nIterateCount; i++)
        {
            outY = k*outY*(-outY);
        }
        outY *= ;

        outZ = z;
    }

    bool IsValidParamA() const {return true;}
    bool IsValidParamB() const {return true;}

private:
    int m_nIterateCount;
};

调节下参数后的图形：

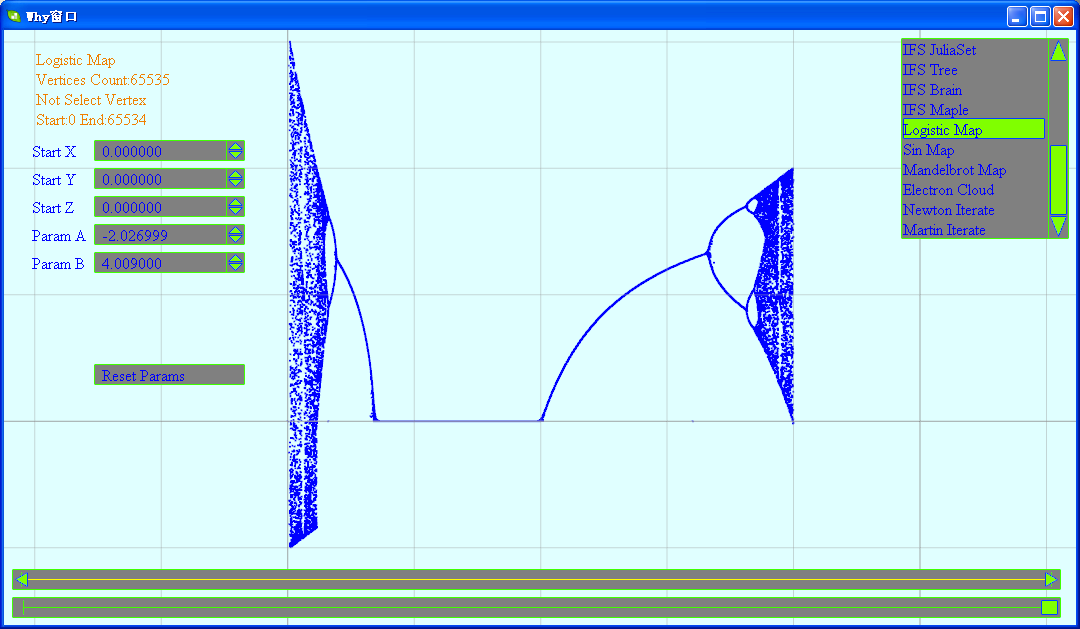
（2）正弦映射系统

// 正弦映射系统
class SinMap : public FractalEquation
{
public:
    SinMap()
    {
        m_StartX = 0.0f;
        m_StartY = 0.0f;
        m_StartZ = 0.0f;

        m_ParamA = -*PI;
        m_ParamB = *PI;

        m_nIterateCount = ;
    }

    void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
    {
        float R = (float)rand()/RAND_MAX;
        float k = m_ParamA + (m_ParamB - m_ParamA) * R;
        outX = R*4.0f;

        outY = (float)rand()/RAND_MAX;
        for (int i = ; i < m_nIterateCount; i++)
        {
            outY = k*sinf(outY);
        }

        outY *= 0.5f;

        outZ = z;
    }

    bool IsValidParamA() const {return true;}
    bool IsValidParamB() const {return true;}

private:
    int m_nIterateCount;
};

（3）曼德勃罗映射系统

// 曼德勃罗映射系统
class MandelbrotMap : public FractalEquation
{
public:
    MandelbrotMap()
    {
        m_StartX = 0.0f;
        m_StartY = 0.0f;
        m_StartZ = 0.0f;

        m_ParamA = -2.0f;
        m_ParamB = 0.0f;

        m_nIterateCount = ;
    }

    void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
    {
        float R = (float)rand()/RAND_MAX;
        float k = m_ParamA + (m_ParamB - m_ParamA) * R;
        outX = R*4.0f;

        outY = (float)rand()/RAND_MAX;
        for (int i = ; i < m_nIterateCount; i++)
        {
            outY = outY*outY + k;
        }

        outZ = z;
    }

    bool IsValidParamA() const {return true;}
    bool IsValidParamB() const {return true;}

private:
    int m_nIterateCount;
};

最后发下被我同事当成MM的逻辑斯蒂分岔图像：

之前我还写过一篇关于逻辑斯蒂的文章：混沌数学之logistic模型