卢卡斯定理 Lucas （p为素数）

证明摘自：（我网上唯一看得懂的证明）

https://blog.csdn.net/alan_cty/article/details/54318369

结论：（显然递归实现）
lucas(n,m)=lucas(n/p,m/p)*C(n%p,m%p)
将n,m很大的数压成求两个小于p的组合数的乘积

数学上的卢卡斯定理两种形式：(n,m用p进制表示)

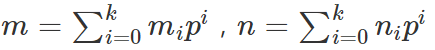
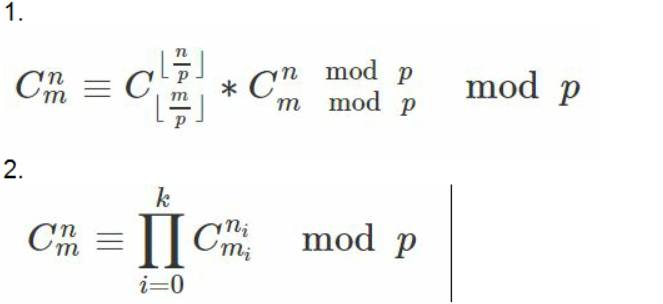
上代码：
 
//打表
void init(ll x){
rec[]=;
For(i,,x)mulmod(rec[i],rec[]*i);
}
//逆元
ll inv(ll x){
return qmul(x,mod-);
}
//求组合数
ll C(ll n,m){
if(n<m)return ;
return rec[n]*inv[rec[m]%mod*inv[n-m]%mod;
}
//卢卡斯
ll lucas(ll n,m){
if(n<m)return ;
ll ans=;
for(;m;n/=mod,m/=mod)
mulmod(ans,C(n%mod,m%mod));
return ans;
}