数学小知识点整理（TBC）

文章目录

• 前言
• 素数与同余
• 线性筛部分
• 素数
• 线性递推逆元
• 指数循环节降幂
• 当求逆元时模数与求逆元的数有可能不互质时的处理方法
• 一个神奇的结论
• 拓展欧拉定理
• 杂乱的一些性质/技巧
• 二进制枚举子集
• 异或前缀和
• O(n)预处理popcount
• 多项式一类
• 组合数学
• 卡特兰数通项
• 斯特林数
• 错排公式
• 二项式反演

前言

感觉距离scoi2019scoi2019scoi2019的时间不多了博主因为太弱所以现在慌得一批，现在尝试梳理一些小知识点顺便复习。

素数与同余

线性筛部分

常识向，直接贴代码了，大佬们手动跳过吧。

最常用的是线性筛质数。

同时有两种常用的可以线性筛预处理的函数：莫比乌斯函数，欧拉函数。

线性筛代码：

typedef long long ll;
ll prime[N],pri[N],cnt=0,mu[N],phi[N];
inline void init(int len){
	mu[1]=phi[1]=1;
	for(int i=2;i<=len;++i){
		if(!pri[i])prime[++cnt]=i,mu[i]=-1,phi[i]=i-1;
		for(int j=1;i*prime[j]<=len;++j){
			pri[i*prime[j]]=1;
			if(i%prime[j]==0){
				phi[i*prime[j]]=phi[i]*prime[j];
				mu[i*prime[j]]=0;
				break;
			}
			mu[k]=-mu[i];
			phi[k]=phi[i]*(prime[j]-1);
		}
	}
}

素数

线性递推逆元

指数循环节降幂

当求逆元时模数与求逆元的数有可能不互质时的处理方法

一个神奇的结论

有个结论，对于 m >= 2，与m的互质的数的和为m * phi (m) / 2

拓展欧拉定理

杂乱的一些性质/技巧

二进制枚举子集

这是一个用循环实现的快速枚举子集的方法，代码如下：

for(int i=s;i;i=s&(i-1))

异或前缀和

一个蒟蒻博主听说可以打表证明的性质：

sumi=i,i≡0mod  4sum_i=i,i\equiv0 \mod4sumi​=i,i≡0mod4

sumi=1,i≡1mod  4sum_i=1,i\equiv1 \mod4sumi​=1,i≡1mod4

sumi=i+1,i≡2mod  4sum_i=i+1,i\equiv2 \mod4sumi​=i+1,i≡2mod4

sumi=0,i≡3mod  4sum_i=0,i\equiv3 \mod4sumi​=0,i≡3mod4

感觉挺有用的

O(n)预处理popcount

popcount(x)popcount(x)popcount(x)指xxx在二进制形式中二进制位为111的数量。

直接处理是O(logx)O(log_x)O(logx​)的，但是可以O(amax)O(a_{max})O(amax​)预处理。

代码：

for(int i=1;i<=lim;++i)Popcount[i]=Popcount[i>>1]+(i&1);

原理很简单（逃

多项式一类

因为太多之前特意写了一篇博客 才不是骗访问量呢

组合数学

卡特兰数通项

Catn=C2nn−C2nn−1=C2nnn+1Cat_n=C_{2n}^n-C_{2n}^{n-1}=\frac{C_{2n}^n}{n+1}Catn​=C2nn​−C2nn−1​=n+1C2nn​​

斯特林数

两类可以用fftfftfft预处理做到O(nlogn)O(nlogn)O(nlogn)

但是一般都只用O(n2)O(n^2)O(n2)（雾

下面给出递推式：

第一类斯特林数递推式：

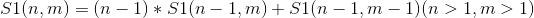
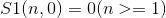
第二类斯特林数递推式：

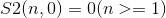
错排公式

看了这道题你就懂了。

递推式：fi=(i−1)(fi−1+fi−2)f_i=(i-1)(f_{i-1}+f_{i-2})fi​=(i−1)(fi−1​+fi−2​)

二项式反演

fn=∑i=0n(ni)gif_n=\sum_{i=0}^n\binom{n}{i}g_ifn​=∑i=0n​(in​)gi​

=>gn=∑i=0n((−1)i(nn−i)fi)g_n=\sum_{i=0}^n((-1)^i\binom{n}{n-i}f_i)gn​=∑i=0n​((−1)i(n−in​)fi​)

可以看这道题简单体会一下。