【bzoj 4173】数学

Description

Input

输入文件的第一行输入两个正整数 。

Output

如题

Sample Input

5 6

Sample Output

240

HINT

N,M<=10^15

题解：

　　之前做的，今天突然留了，想起了就补上。

　　首先对于 m%k+n%k>=k
　　那么设m=a1*k+b1,n=a2*k+b2;

　　 m%k+n%k>=k ===> (a1+a2)*k+b1+b2>=(a1+a2+1)*k  

　　即 (a1*k+b1)+(a2*k+b2)>=(a1+a2)*k+k

　　同除k向下取整，即

　　       

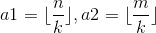
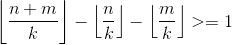　　，然后考虑不等式前面式子只有两种结果，0或1。先不考虑φ（n）和φ（m）。

　　那么原题面后面的式子可以转化为

　　，再设　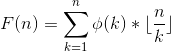　，答案就变成了F（n+m）-F(n)-F(m);

　　在考虑如何求F(n）；

　　,

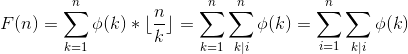　　然后又已知

　　，

　　所以

　　。

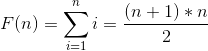　　结果就是:

　　

代码就不贴了= =