数据结构和算法总结（一）：广度优先搜索BFS和深度优先搜索DFS

前言

这几天复习图论算法，觉得BFS和DFS挺重要的，而且应用比较多，故记录一下。

广度优先搜索

有一个有向图如图a

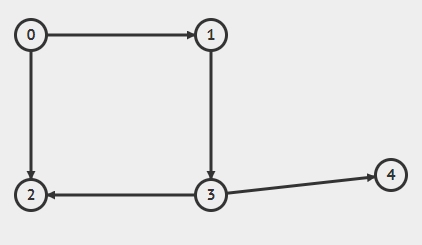
图a

广度优先搜索的策略是：

从起始点开始遍历其邻接的节点，由此向外不断扩散。

1.假设我们以顶点0为原点进行搜索，首先确定邻接0的顶点集合S0 = {1，2}。

2.然后确定顶点1的集合S1 = {3}，顶点2没有邻接点，所以集合为空。

3.然后确定3的邻接点集合S3，因为2已经被遍历过，所以不考虑，所以由顶点3知道的邻接点集合S3 = {4}。

4.然后再确定顶点4的邻接点集合,顶点4没有更多的邻接点了，此时也没有还未遍历的邻接点集合，搜索终止。

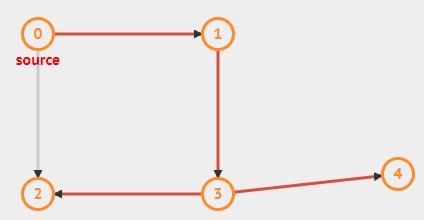
遍历的路径可以参考如下图红色标记的路径：

动态过程

代码的实现思路：

BFS()
{
  输入起始点；
  初始化所有顶点标记为未遍历；
  初始化一个队列queue并将起始点放入队列；
 
  while（queue不为空）
  {
    从队列中删除一个顶点s并标记为已遍历；
    将s邻接的所有还没遍历的点加入队列；
  }
}

深度优先遍历

继续以图a为例

图a

深度优先遍历的策略是：

从一个顶点v出发，首先将v标记为已遍历的顶点，然后选择一个邻接于v的尚未遍历的顶点u，如果u不存在，本次搜素终止。如果u存在，那么从u又开始一次DFS。如此循环直到不存在这样的顶点。

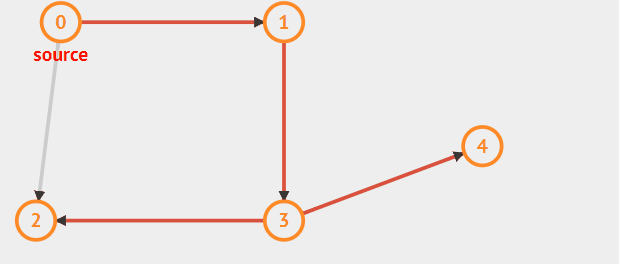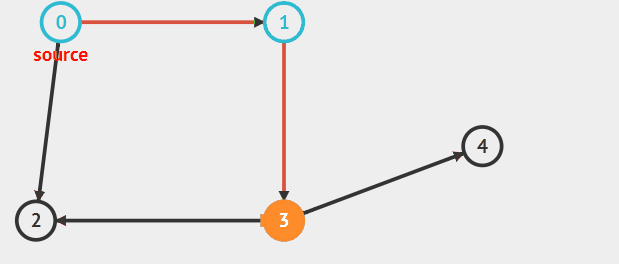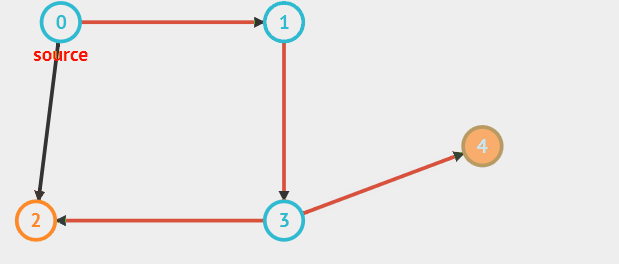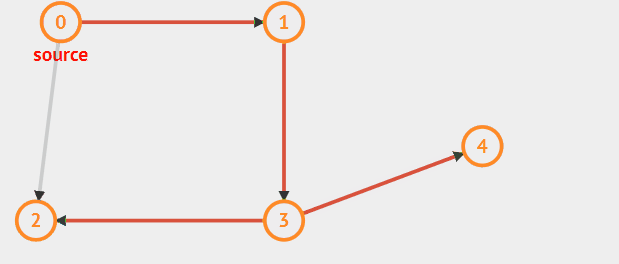
比如图a中

1.从顶点0开始，将0标记为已遍历，然后选择未被遍历的邻接0的顶点1。

2.标记顶点1，然后选择3并标记，然后选择顶点3邻接的顶点2。

3.顶点2标记后没有与它邻接的未标记的点，所以返回3选择另一个邻接3并且未被标记的顶点4。

4.顶点4没有更多的符合条件的点，因此搜索终止，返回到3，3没有更多的点，搜索终止返回到1，最后返回到0，搜索终止。

遍历的路径可以参考如下图红色标记的路径：

动态过程

代码的实现思路：

DFS（顶点v）
{
  标记v为已遍历；
  for（对于每一个邻接v且未标记遍历的点u）
      DFS（u）;
}

一个简单的应用

问题不赘述，具体可参考   LeetCode朋友圈问题  。

实现的代码如下（C#）：

public class Solution {
    public void dfs(int [,]M,int []visit,int i)
    {
        for(int j = ;j < M.GetLength();j++)
        {
            if(M[i,j] ==  && visit[j] == )
            {
                visit[j] = ;
                dfs(M,visit,j);
            }
        }
    }
 
    public void bfs(int [,]M,int []visit,int i)
    {
        Queue<int> q = new Queue<int>();
        q.Enqueue(i);
        while(q.Count > )
        {
            int temp = q.Dequeue();
            for(int j = ;j < M.GetLength();j++)
            {
                if(M[temp,j] ==  && visit[j] == )
                {
                    visit[j] = ;
                    q.Enqueue(j);
                }
            }
        }
    }
 
    public int FindCircleNum(int[,] M) {
        int N = M.GetLength();
        int circle = ; //朋友圈数
        int[] visit = new int[N];
        for(int i = ;i < N;i++)
        {
            if(visit[i] == ) //还没被遍历过
            {
                //dfs(M,visit,i); //使用dfs搜索并标记与其相关的学生
                bfs(M,visit,i);   //使用bfs搜索并标记与其相关的学生
                circle++;
            }
        }
        return circle;
    }
}

参考资料

《数据结构、算法与应用——C++描述》   作者：【美】 萨特吉·萨尼       机械工业出版社

Visualgo算法可视化网站