Pytorch中torch.autograd ---backward函数的使用方法详细解析，具体例子分析

backward函数

官方定义：

torch.autograd.backward(tensors, grad_tensors=None, retain_graph=None, create_graph=False, grad_variables=None)

Computes the sum of gradients of given tensors w.r.t. graph leaves.The graph is differentiated using the chain rule. If any of tensors are non-scalar (i.e. their data has more than one element) and require gradient, the function additionally requires specifying grad_tensors. It should be a sequence of matching length, that contains gradient of the differentiated function w.r.t. corresponding tensors (None is an acceptable value for all tensors that don’t need gradient tensors). This function accumulates gradients in the leaves - you might need to zero them before calling it.

翻译和解释：参数tensors如果是标量,函数backward计算参数tensors对于给定图叶子节点的梯度（ graph leaves，即为设置requires_grad=True的变量）。

参数tensors如果不是标量，需要另外指定参数grad_tensors，参数grad_tensors必须和参数tensors的长度相同。在这一种情况下，backward实际上实现的是代价函数（loss = torch.sum(tensors*grad_tensors); 注：torch中向量*向量实际上是点积，因此tensors和grad_tensors的维度必须一致 ）关于叶子节点的梯度计算，而不是参数tensors对于给定图叶子节点的梯度。如果指定参数grad_tensors=torch.ones((size(tensors))),显而易见，代价函数关于叶子节点的梯度，也就等于参数tensors对于给定图叶子节点的梯度。

每次backward之前，需要注意叶子梯度节点是否清零，如果没有清零，第二次backward会累计上一次的梯度。

下面给出具体的例子：

 import torch
 x=torch.randn((3),dtype=torch.float32,requires_grad=True)
 y = torch.randn((3),dtype=torch.float32,requires_grad=True)
 z = torch.randn((3),dtype=torch.float32,requires_grad=True)
 t = x + y
 loss = t.dot(z)  #求向量的内积

在调用 backward 之前，可以先手动求一下导数，应该是：

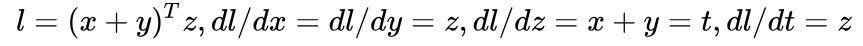
用代码实现求导：

 loss.backward(retain_graph=True)
 print(z,x.grad,y.grad)  #预期打印出的结果都一样
 print(t,z.grad)    #预期打印出的结果都一样
 print(t.grad)    #在这个例子中，x,y,z就是叶子节点，而t不是，t的导数在backward的过程中求出来回传之后就会被释放,因而预期结果是None

结果和预期一致：

tensor([-2.6752,  0.2306, -0.8356], requires_grad=True) tensor([-2.6752,  0.2306, -0.8356]) tensor([-2.6752,  0.2306, -0.8356])
tensor([-1.1916, -0.0156,  0.8952], grad_fn=<AddBackward0>) tensor([-1.1916, -0.0156,  0.8952])
None

敲重点：注意到前面函数的解释中，在参数tensors不是标量的情况下，tensor.backward(grad_tensors)实现的是代价函数（torch.sum(tensors*grad_tensors)）关于叶子节点的导数。在上面例子中，loss = t.dot(z)，因此用t.backward(z),实现的就是loss对于所有叶子结点的求导，实际运算结果和预期吻合。

 t.backward(z,retain_graph=True)
 print(z,x.grad,y.grad)
 print(t,z.grad)

运行结果如下：

tensor([-0.7830,  1.4468,  1.2440], requires_grad=True) tensor([-0.7830,  1.4468,  1.2440]) tensor([-0.7830,  1.4468,  1.2440])
tensor([-0.7145, -0.7598,  2.0756], grad_fn=<AddBackward0>) None

上面的结果中，出现了一个问题，虽然loss关于x和y的导数正确，但是z不再是叶子节点了。

问题1：当使用t.backward(z,retain_graph=True)的时候， print(z.grad)结果是None,这意味着z不再是叶子节点，这是为什么呢？

另外一个尝试，loss = t.dot(z)=z.dot(t),但是如果用z.backward(t)替换t.backward(z,retain_graph=True)，结果却不同。

 z.backward(t)
 print(z,x.grad,y.grad)
 print(t,z.grad)

运行结果：

tensor([-1.0716, -1.3643, -0.0016], requires_grad=True) None None
tensor([-0.7324,  0.9763, -0.4036], grad_fn=<AddBackward0>) tensor([-0.7324,  0.9763, -0.4036])

问题2：上面的结果中可以看到，使用z.backward(t)，x和y都不再是叶子节点了，z仍然是叶子节点，且得到的loss相对于z的导数正确。

上述仿真出现的两个问题，我还不能解释，希望和大家交流，我的邮箱yangyuwen_yang@126.com，欢迎来信讨论。

问题1：当使用t.backward(z,retain_graph=True)的时候， print(z.grad)结果是None,这意味着z不再是叶子节点，这是为什么呢？

问题2：上面的结果中可以看到，使用z.backward(t)，x和y都不再是叶子节点了，z仍然是叶子节点，且得到的loss相对于z的导数正确。

---

另外强调一下，每次backward之前，需要注意叶子梯度节点是否清零，如果没有清零，第二次backward会累计上一次的梯度。
简单的代码可以看出：

 #测试1,：对比上两次单独执行backward，此处连续执行两次backward
 t.backward(z,retain_graph=True)
 print(z,x.grad,y.grad)
 print(t,z.grad)
 z.backward(t)
 print(z,x.grad,y.grad)
 print(t,z.grad)
 # 结果x.grad,y.grad本应该是None，因为保留了第一次backward的结果而打印出上一次梯度的结果

tensor([-0.5590, -1.4094, -1.5367], requires_grad=True) tensor([-0.5590, -1.4094, -1.5367]) tensor([-0.5590, -1.4094, -1.5367])
tensor([-1.7914, 0.8761, -0.3462], grad_fn=<AddBackward0>) None
tensor([-0.5590, -1.4094, -1.5367], requires_grad=True) tensor([-0.5590, -1.4094, -1.5367]) tensor([-0.5590, -1.4094, -1.5367])
tensor([-1.7914, 0.8761, -0.3462], grad_fn=<AddBackward0>) tensor([-1.7914, 0.8761, -0.3462])

 #测试2,：连续执行两次backward，并且清零，可以验证第二次backward没有计算x和y的梯度
 t.backward(z,retain_graph=True)
 print(z,x.grad,y.grad)
 print(t,z.grad)
 x.grad.data.zero_()
 y.grad.data.zero_()
 z.backward(t)
 print(z,x.grad,y.grad)
 print(t,z.grad)

tensor([ 0.8671, 0.6503, -1.6643], requires_grad=True) tensor([ 0.8671, 0.6503, -1.6643]) tensor([ 0.8671, 0.6503, -1.6643])
tensor([1.6231e+00, 1.3842e+00, 4.6492e-06], grad_fn=<AddBackward0>) None
tensor([ 0.8671, 0.6503, -1.6643], requires_grad=True) tensor([0., 0., 0.]) tensor([0., 0., 0.])
tensor([1.6231e+00, 1.3842e+00, 4.6492e-06], grad_fn=<AddBackward0>) tensor([1.6231e+00, 1.3842e+00, 4.6492e-06])

附参考学习的链接如下，并对作者表示感谢：
PyTorch 的 backward 为什么有一个 grad_variables 参数？该话题在我的知乎专栏里同时转载，欢迎更多讨论交流，参见链接。