【BJOI2014】大融合【LCT】

闲着没事写篇题解

传送门

LCT维护子树的模板题

树链剖分中，子树可以用dfs序维护。但LCT你总不可能动态维护dfs序啊

LCT之所以不能直接维护子树，是因为LCT只能维护它的重儿子。我们把这棵子树称为重子树。

对于其他子树，我们称为轻子树。轻子树只会储存父节点，要不试试在跑fa的时候顺便维护轻子树？

以此题为例，设s[i]为整棵子树的大小，si[i]为虚子树大小

这里的虚子树指所有虚边连向它的儿子的大小(即s)的和

不难看出，我们询问x，y时

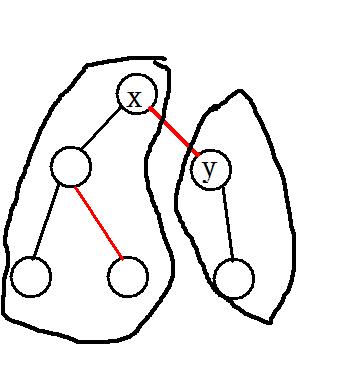
实际上是求(si[x]+1)(si[y]+1)

如何维护s和si？

我们发现，只有当改变了树的形态的时候，才会对s和si产生影响

access：会改变。直接在接头的时候顺便改一下

	void access(int x)
	{
		for (int y=0;x;y=x,x=fa[x])
		{
			splay(x);
			si[x]+=s[ch[x][1]];
			si[x]-=s[ch[x][1]=y];
			pushup(x);
		}
	}

makeroot:虽然改了，其实只是改了下顺序，access和splay里面会改

split：没有，下一个

link和cut：link把父亲的si加一下，cut把父亲的s和si都减一下

（实际上就是直接调用了fa或ch的函数）

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cctype>
#define MAXN 100005
using namespace std;
namespace Splay
{
	int ch[MAXN][2],fa[MAXN];
	int rv[MAXN];
	int si[MAXN],s[MAXN];
	void pushup(int x)
	{
		s[x]=s[ch[x][0]]+s[ch[x][1]]+si[x]+1;
	}
	void pushr(int x)
	{
		swap(ch[x][0],ch[x][1]);
		rv[x]^=1;
	}
	void pushdown(int x)
	{
		if (rv[x])
		{
			if (ch[x][0]) pushr(ch[x][0]);
			if (ch[x][1]) pushr(ch[x][1]);
			rv[x]=0;
		}
	}
	bool isroot(int x)
	{
		return ch[fa[x]][0]!=x&&ch[fa[x]][1]!=x;
	}
	bool get(int x)
	{
		return ch[fa[x]][1]==x;
	}
	void rotate(int x)
	{
		int y=fa[x],z=fa[y];
		int l=get(x),r=l^1;
		int w=ch[x][r];
		if (!isroot(y))
			ch[z][get(y)]=x;
		ch[x][r]=y;
		ch[y][l]=w;
		if (w)
			fa[w]=y;
		fa[y]=x;
		fa[x]=z;
		pushup(y);
		pushup(x);
	}
	int q[MAXN],top;
	void splay(int x)
	{
		q[top=1]=x;
		for (int i=x;!isroot(i);i=fa[i])
			q[++top]=fa[i];
		for (int i=top;i>=1;i--)
			pushdown(q[i]);
		while (!isroot(x))
		{
			int y=fa[x];
			if (!isroot(y))
			{
				if (get(x)==get(y))
					rotate(y);
				else
					rotate(x);
			}
			rotate(x);
		}
		pushup(x);
	}
}
using namespace Splay;
namespace LCT
{
	void access(int x)
	{
		for (int y=0;x;y=x,x=fa[x])
		{
			splay(x);
			si[x]+=s[ch[x][1]];
			si[x]-=s[ch[x][1]=y];
			pushup(x);
		}
	}
	void evert(int x)
	{
		access(x);
		splay(x);
		pushr(x);
	}
	void split(int x,int y)
	{
		evert(x);
		access(y);
		splay(y);
	}
	void link(int x,int y)
	{
		split(x,y);
		si[fa[x]=y]+=s[x];
		pushup(y);
	}
}
using namespace LCT;
inline int read()
{
	int ans=0;
	char c=getchar();
	while (!isdigit(c))
		c=getchar();
	while (isdigit(c))
		ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
	return ans;
}
inline char getalpha()
{
	char c=getchar();
	while (!isalpha(c))
		c=getchar();
	return c;
}
int main()
{
	int n,q;
	n=read(),q=read();
	for (int i=1;i<=n;i++)
		s[i]=1;
	while (q--)
	{
		char c=getalpha();
		int x,y;
		x=read(),y=read();
		if (c=='A')
			link(x,y);
		else
		{
			split(x,y);
			printf("%I64d\n",(long long)(si[x]+1)*(si[y]+1));
		}
	}
	return 0;
}