KVC, KVO 实现原理

Key-Value Coding: 键值编码 (KVC)

方法调用:

// 对象属性
// 类似: Person -> name
setValue: forKey:
// 对象的属性或者 属性的属性...... 可见它已经包含前者.
// 类似: Person -> car -> name
setValue: forKeyPath:

KVC运用了一个isa-swizzling技术. isa-swizzling就是类型混合指针机制, 将2个对象的isa指针互相调换, 就是俗称的黑魔法.

KVC主要通过isa-swizzling, 来实现其内部查找定位的. 默认的实现方法由NSOject提供

　　isa指针, 如其名称所指,(就是is a kind of的意思), 指向分发表对象的类. 该分发表实际上包含了指向实现类中的方法的指针, 和其它数据。

比如说如下的一行KVC的代码：

[object setValue:@"" forKey:@"uid"];

就会被编译器处理成:
// 首先找到对应sel
SEL sel = sel_get_uid("setValue:forKey:");
// 根据object->isa找到sel对应的IMP实现指针
IMP method = objc_msg_lookup (object->isa,sel);
// 调用指针完成KVC赋值
method(object, sel, @"", @"uid");

KVC键值查找原理

setValue:forKey:搜索方式

、首先搜索setKey:方法.(key指成员变量名, 首字母大写)
、上面的setter方法没找到, 如果类方法accessInstanceVariablesDirectly返回YES. 那么按 _key, _isKey，key, iskey的顺序搜索成员名.(NSKeyValueCodingCatogery中实现的类方法, 默认实现为返回YES)
、如果没有找到成员变量, 调用setValue:forUnderfinedKey:

valueForKey:的搜索方式

、首先按getKey, key, isKey的顺序查找getter方法, 找到直接调用. 如果是BOOL、int等内建值类型, 会做NSNumber的转换.
、上面的getter没找到, 查找countOfKey, objectInKeyAtindex, KeyAtindexes格式的方法. 如果countOfKey和另外两个方法中的一个找到, 那么就会返回一个可以响应NSArray所有方法的代理集合的NSArray消息方法.
、还没找到, 查找countOfKey, enumeratorOfKey, memberOfKey格式的方法. 如果这三个方法都找到, 那么就返回一个可以响应NSSet所有方法的代理集合.
、还是没找到, 如果类方法accessInstanceVariablesDirectly返回YES. 那么按 _key, _isKey, key, iskey的顺序搜索成员名.
、再没找到, 调用valueForUndefinedKey.

Key-Value Observing 键值观察(KVO), KVO是观察者模式的一种应用

观察者思想:

一个目标对象管理所有依赖于它的观察者对象，并在它自身的状态改变时主动通知观察者对象。这个主动通知通常是通过调用各观察者对象所提供的接口方法来实现的。观察者模式较完美地将目标对象与观察者对象解耦。

方法调用

// 添加一个观察者
[self.object addObserver:self forKeyPath:@"uid" options:NSKeyValueObservingOptionOld|NSKeyValueObservingOptionNew context:nil];

// 观察者监听到之后回调方法
- (void)observeValueForKeyPath:(NSString *)keyPath ofObject:(id)object change:(NSDictionary<NSString *,id> *)change context:(void *)context {
    NSLog(@"keyPath: %@", keyPath);
    NSLog(@"object: %@", object);
    NSLog(@"change: %@", change);
    NSLog(@"context: %@", context);
}

// 移除观察者, 类在销毁前需要销毁
[self.object removeObserver:self forKeyPath:@"uid"];

由此可见, 只有当我们调用KVC去访问key值的时候KVO才会起作用. 所以肯定确定的是, KVO是基于KVC实现的,

系统实现KVO有以下几个步骤：

• 当类A的对象第一次被观察的时候，系统会利用运行时动态创建与类A一样的NSKVONotifying_A派生类, 并且只有1个属性的get, set方法实现.
• 在派生类NSKVONotifying_A中重写类A的setter方法，NSKVONotifying_A类在被重写的setter方法中实现通知机制。
• 类NSKVONotifying_A重写会 class方法，将自己伪装成类A。类NSKVONotifying_A还会重写dealloc方法释放资源。
• 系统将所有指向类A对象的isa指针指向类NSKVONotifying_A的对象。

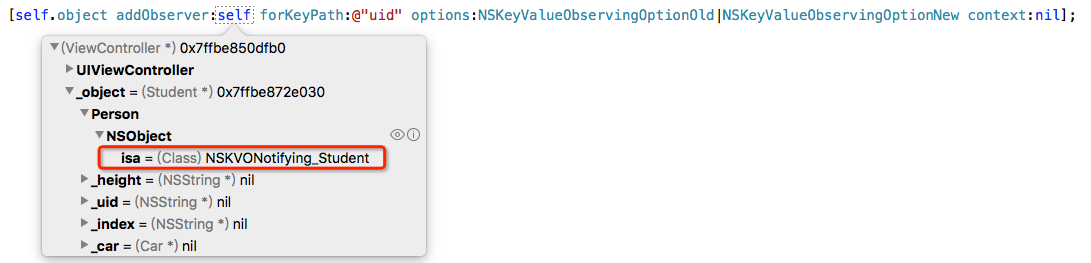
下面就是在调用KVO过程中object对象的isa指针指向

在没有添加观察者之前 isa 指向的是Student类

在添加完观察者之后, isa指针指向了NSKVONotifying_Student类, 所以能肯定NSKVONotifying_Student 是后来被创建出来作为监听用的