欧拉工程第69题：Totient maximum

题目链接

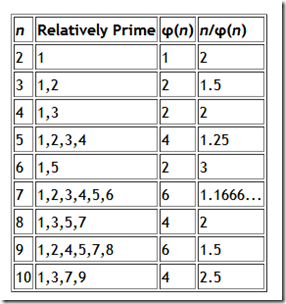
欧拉函数φ(n)（有时也叫做phi函数）可以用来计算小于n 的数字中与n互质的数字的个数。

当n小于1，000,000时候，n/φ(n)最大值时候的n。

欧拉函数维基百科链接

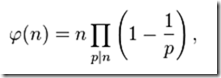
这里的是p是n的素因子，当素因子有相同的时候只取一个

任意一个正整数都能分解成若干个素数乘积的形式

如下所示：

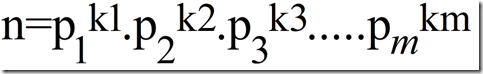
long phi(int n){
        long res=0;
        int pi=0;
        if(n==1) return 0;
        res = n;
        pi = 2;
        while(n!=1){
            if(n%pi==0){
                res*=(pi-1);
                res/=pi;
                while(n%pi==0){
                    n/=pi;
                }
            }
            pi++;
        }
    return res;
    }

上面res是存放φ(n)

是素因子的数更行res

由于素因子可能相同的

while(n%pi==0){
                    n/=pi;
                }

这里的while循环就是用来去除重复的素因子

然而运行结果：

//    510510 5.539388020833333
//    running time=270s483ms

这里要变量一百万次，内循环还要遍历，时间已经超过了欧拉工程的一分钟原则

参考网上程序，改成下面的形式：

long phi2(int n){
        long res = 0;
        if(n==1) return 0;
        int pi=2;
        res = n;
        while(pi*pi <=n){
            if(n%pi==0){
                res*=(pi-1);
                res/=pi;
                while(n%pi==0){
                    n/=pi;
                }
                }
            pi++;
        }
        if(n>1){
            res*=(n-1);
            res/=n;
        }
        return res;
    }

一个结束条件是while(n!=1)

一个结束条件是while(pi*pi<=n)  n的素因子一定小于等于根号n，当pi大于根号n的时候的循环完全是拜拜浪费时间

此时你一定想到素数的循环，这里很类似

运行结果：

//    510510 5.539388020833333
//    running time=1s292ms

时间少了很多

在题解报告中，看到用到素数

当这个数的是素数的时候，欧拉函数φ(n) = n-1

当不是素数时候，找出小于n的素数，且能不n整除的数是n的素因子

long phi3(int n){
        long res = n;
        int pi=2;
        if(isPrime(n)||n==1)
            res = n-1;
        else{
            while(pi<=n){
                if(n%pi==0 &&isPrime(pi)){
                    res*=(pi-1);
                    res/=pi;
                }
                pi++;
            }

        }
        return res;

    }

结果：

//    510510 5.539388020833333
//    running time=1885s497ms

上面程序对找到的素因子，没有去除，同时循环是while(pi<=n),可以进一步优化

while(pi<=n){
                if(n%pi==0 &&isPrime(pi)){
                    res*=(pi-1);
                    res/=pi;
                    while(n%pi==0){
                        n/=pi;
                    }
                }
                pi++;
            }

结果：

//    510510 5.539388020833333
//    running time=111s291ms

时间少了好多

while(pi*pi<=n){
                if(n%pi==0 &&isPrime(pi)){
                    res*=(pi-1);
                    res/=pi;
//                    while(n%pi==0){
//                        n/=pi;
//                    }
                }
                pi++;
            }

结果：

//    510510 5.539388020833333
//    running time=4s531ms

然而while（pi*pi<=n） + 去除相同素因子 的，程序结果不对！！！

while(pi*pi<=n){
                if(n%pi==0 &&isPrime(pi)){
                    res*=(pi-1);
                    res/=pi;
                    while(n%pi==0){
                        n/=pi;
                    }
                }
                pi++;
            }
            if(n>1) res = res/n*(n-1);

这样就对了

结果：

//    510510 5.539388020833333
//    running time=1s454ms

去重后，最后一个n也是符合条件的

这个时间竟然比第2个的时间还要长。

Python程序：

import time as time

def phi(n):
    if n==1 :return 0
    res = n
    pi = 2
    while(pi*pi<=n):
        if n%pi==0:
            res=res/pi*(pi-1)
            while n%pi==0:
                n/=pi
        pi+=1
    if n>1:res=res/n*(n-1)
    return res
# 510510
# running time: 32.007999897 s
if __name__ == '__main__':
    t0 = time.time()
    Max_n = 1000000
    result= 1
    value = 0.0
    for n in range(2,Max_n):
        euler = phi(n)
        temp = n/(euler*1.0)
        if temp>value:
            value = temp
            result = n
    print result
    print "running time:",(time.time() - t0),'s'

全部的Java程序：

package project61;

public class P69{

    void run(){

        long max_n = 1000000;
        double value = 0.0;
        long euler = 0;
        long N=0;

        for(int i=2;i<=max_n;i++){

            euler = phi3(i);
//            System.out.println(i+" "+euler);
            double temp = (double)i/(euler*1.0);
                if(temp>value){
                    value = temp;
                    N = i;
                }

        }
        System.out.println(N+" "+value);
    }
    long phi3(int n){
        long res = n;
        int pi=2;
        if(isPrime(n)||n==1)
            res = n-1;
        else{
            while(pi*pi<=n){
                if(n%pi==0 &&isPrime(pi)){
                    res*=(pi-1);
                    res/=pi;
                    while(n%pi==0){
                        n/=pi;
                    }
                }
                pi++;
            }
            if(n>1) res = res/n*(n-1);
        }
        return res;

    }
//    510510 5.539388020833333
//    running time=1885s497ms

//    510510 5.539388020833333
//    running time=111s291ms

//    510510 5.539388020833333
//    running time=4s531ms

//    510510 5.539388020833333
//    running time=1s454ms
    boolean isPrime(int num){
        if(num==2||num==3||num==5||num==7) return true;
        if(num<=1||num%2==0||num%3==0) return false;
        for(int i=2;i<=Math.sqrt(num)+1;i++){
            if(num%i==0) return false;
        }
        return true;
    }
    long phi2(int n){
        long res = 0;
        if(n==1) return 0;
        int pi=2;
        int k =0;
        res = n;
        while(pi*pi <=n){
            if(n%pi==0){
                res*=(pi-1);
                res/=pi;
                while(n%pi==0){
                    n/=pi;
                }
                }
            pi++;
        }
        if(n>1){
            res*=(n-1);
            res/=n;
        }
        return res;
    }
//    510510 5.539388020833333
//    running time=1s292ms

    long phi(int n){
        long res=0;
        int pi=0;
        if(n==1) return 0;
        res = n;
        pi = 2;
        while(n!=1){
            if(n%pi==0){
                res*=(pi-1);
                res/=pi;
                while(n%pi==0){
                    n/=pi;
                }
            }
            pi++;
        }
    return res;
    }
//    510510 5.539388020833333
//    running time=270s483ms

    public static void main(String[] args){
        long start = System.currentTimeMillis();
        new P69().run();
        long end = System.currentTimeMillis();
        long time = end - start;
        System.out.println("running time="+time/1000+"s"+time%1000+"ms");

    }
}