BFS+优先队列+状态压缩DP+TSP

http://acm.hdu.edu.cn/showproblem.php?pid=4568

Hunter

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 1254    Accepted Submission(s): 367

Problem Description

　　One day, a hunter named James went to a mysterious area to find the treasures. James wanted to research the area and brought all treasures that he could.

　　The area can be represented as a N*M rectangle. Any points of the rectangle is a number means the cost of research it,-1 means James can't cross it, James can start at any place out of the rectangle, and explore point next by next. He will move in the rectangle
and bring out all treasures he can take. Of course, he will end at any border to go out of rectangle(James will research every point at anytime he cross because he can't remember whether the point are researched or not).

　　Now give you a map of the area, you must calculate the least cost that James bring out all treasures he can take(one point up to only one treasure).Also, if nothing James can get, please output 0.

 

Input

　　The input consists of T test cases. The number of test cases T is given in the first line of the input. Each test case begins with a line containing 2 integers N M , (1<=N,M<=200), that represents the rectangle. Each of the following
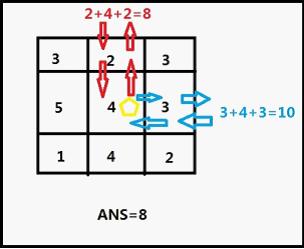
N lines contains M numbers(0~9),represent the cost of each point. Next is K(1<=K<=13),and next K lines, each line contains 2 integers x y means the position of the treasures, x means row and start from 0, y means column start from 0 too.

 

Output

　　For each test case, you should output only a number means the minimum cost.

 

Sample Input

2
3 3
3 2 3
5 4 3
1 4 2
1
1 1
3 3
3 2 3
5 4 3
1 4 2
2
1 1
2 2

 

Sample Output

8
11

 

题意：给一个n行m列的迷宫，每个格子都有数字代表花费，-1代表这个格子无法通过，然后给出k个放有宝石的格子的坐标，每个格子最多有一个宝石，问从边缘进入迷宫拿出所有的所有的宝石再从边缘出去的最小花费，每个格子可以走多次；

分析：首先这道题题意特蛋疼，首先这种情况：

5 5

1 1 1 1 1

1 -1 -1 -1 -1

1 -1 1 1 1

1 -1 1 1 1

1 -1 1 1 1

2

0 0

4 4

两个宝石完全被隔开，如果只进出一次是没办法全部拿出来的，可以进出多次的话可以，但是题目中也没说是不是只能进入一次，加入只能进入一次，但是拿不完输出什么，题目中也没有说，还有一种情况：

5 5

1 1 1 1 1

1 -1 -1 -1 1

1 -1 1 -1 1

1 -1 -1 -1 1

1 1 1 1 1

1

2 2

无论怎么拿都拿不出来，此时应该输出0吗，但是你只有进去了才知道拿不出完，只要进去了就有花费应该怎么输出呢？费解。。。。。。

但是以上测试数据时没有的，那这就简单了；

首先BFS+优先队列，求出宝石之间的最短距离，顺便求出每个宝石到边缘的距离，存在dist中，注意dist包含两个端点的费用，然后把两端的费用去掉放在dis中，接下来就是典型的TSP问题了，用状压DP求拿出所有宝石的状态即可；

最后的结果+所有宝石的费用；

#include"stdio.h"
#include"string.h"
#include"iostream"
#include"map"
#include"string"
#include"queue"
#include"stdlib.h"
#include"algorithm"
#include"math.h"
#define M (1<<15)+2
#define eps 1e-10
#define inf 100000000
#define mod 100000000
#define INF 0x3f3f3f3f
using namespace std;
int dp[M][17],dist[222][222],use[222][222],vis[222][222];
int mp[222][222],px[20];
int dis[17][17];
int disx[5]={0,1,0,-1};
int disy[5]={1,0,-1,0};
int n,m;
struct node
{
    int x,y,t;
    friend bool operator<(node a,node b)
    {
        return a.t>b.t;
    }
};
int min(int a,int b)
{
    return a<b?a:b;
}
int bfs(int x,int y)
{
    int mini=INF,i;
    priority_queue<node>q;
    memset(dist,INF,sizeof(dist));
    memset(vis,0,sizeof(vis));
    node now;
    now.x=x;
    now.y=y;
    now.t=mp[x][y];
    vis[now.x][now.y]=1;
    q.push(now);
    while(!q.empty())
    {
        node cur=q.top();
        q.pop();
        for(i=0;i<4;i++)
        {
            now.x=cur.x+disx[i];
            now.y=cur.y+disy[i];
            if(now.x<0||now.y<0||now.x>=n||now.y>=m)
            {
                if(mini>cur.t)
                    mini=cur.t;
                continue;
            }
            if(mp[now.x][now.y]==-1)continue;
            now.t=cur.t+mp[now.x][now.y];
            if(dist[now.x][now.y]>now.t)
            {
                dist[now.x][now.y]=now.t;
                if(!vis[now.x][now.y])
                {
                    vis[now.x][now.y]=1;
                    q.push(now);
                }
            }
            if(now.x==0||now.y==0||now.x==n-1||now.y==m-1)
            {
                if(mini>now.t)
                    mini=now.t;
            }

        }
    }
    return mini;
}
void DP(int cnt)
{
    int i,j,k;
    memset(dp,INF,sizeof(dp));
    dp[1][0]=0;
    dp[1<<(cnt-1)][cnt-1]=0;
    int ff=0;
    ff|=1;
    ff|=1<<(cnt-1);
    for(i=1;i<px[cnt];i++)
    {
        if((i&ff)==0)continue;
        for(j=0;j<cnt;j++)
        {
            int tep=i&(1<<j);
            if(tep==0)continue;
            int cur=i^(1<<j);
            for(k=0;k<cnt;k++)
            {
                if((cur&(1<<k))==0||k==j)continue;
                if(dp[cur][k]>=INF||dis[k][j]>=INF)continue;
                if(dp[i][j]>dp[cur][k]+dis[k][j])
                    dp[i][j]=dp[cur][k]+dis[k][j];
            }
        }
    }
}
struct Node
{
    int x,y,val;
}p[20];
int main()
{
    int T,i,j,fuck,x,y;
    px[0]=1;
    for(i=1;i<=15;i++)
        px[i]=px[i-1]*2;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d",&n,&m);
        for(i=0;i<n;i++)
            for(j=0;j<m;j++)
                scanf("%d",&mp[i][j]);
        scanf("%d",&fuck);
        int cnt=1;
        int ans=0;
        for(i=0;i<fuck;i++)
        {
            scanf("%d%d",&x,&y);
            ans+=mp[x][y];
            p[cnt].x=x;
            p[cnt].y=y;
            p[cnt].val=mp[x][y];
            cnt++;
        }
        memset(dis,INF,sizeof(dis));
        for(i=1;i<cnt;i++)
        {
            int L=bfs(p[i].x,p[i].y);
            if(L<INF)
            dis[0][i]=dis[i][0]=dis[i][cnt]=dis[cnt][i]=L-mp[p[i].x][p[i].y];
            for(j=1;j<cnt;j++)
            {
                if(i==j)dis[i][j]=INF;
                else
                {
                    if(dist[p[j].x][p[j].y]<INF)
                    dis[i][j]=dist[p[j].x][p[j].y]-mp[p[i].x][p[i].y]-mp[p[j].x][p[j].y];
                }
            }
        }
        cnt++;
        DP(cnt);
        if(dp[px[cnt]-1][0]<INF)
        printf("%d\n",ans+dp[px[cnt]-1][0]);
        else
            printf("0\n");
    }
}