Code Forces 149DColoring Brackets(区间DP)

 Coloring Brackets

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Once Petya read a problem about a bracket sequence. He gave it much thought but didn't find a solution. Today you will face it.

You are given string s. It represents a correct bracket sequence. A correct bracket sequence is the sequence of opening ("(")
and closing (")") brackets, such that it is possible to obtain a correct mathematical expression from it, inserting numbers and operators between the brackets.
For example, such sequences as "(())()" and "()" are correct
bracket sequences and such sequences as ")()" and "(()" are
not.

In a correct bracket sequence each bracket corresponds to the matching bracket (an opening bracket corresponds to the matching closing bracket and vice versa). For example, in a bracket sequence shown of the figure below, the third bracket corresponds to the
matching sixth one and the fifth bracket corresponds to the fourth one.

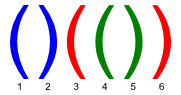
You are allowed to color some brackets in the bracket sequence so as all three conditions are fulfilled:

• Each bracket is either not colored any color, or is colored red, or is colored blue.
• For any pair of matching brackets exactly one of them is colored. In other words, for any bracket the following is true: either it or the matching bracket that corresponds to it is colored.
• No two neighboring colored brackets have the same color.

Find the number of different ways to color the bracket sequence. The ways should meet the above-given conditions. Two ways of coloring are considered different if they differ in the color of at least one bracket. As the result can be quite large, print it modulo 1000000007 (109 + 7).

Input

The first line contains the single string s (2 ≤ |s| ≤ 700)
which represents a correct bracket sequence.

Output

Print the only number — the number of ways to color the bracket sequence that meet the above given conditions modulo 1000000007 (109 + 7).

Examples

input

(())

output

12

input

(()())

output

40

input

()

output

4

区间DP

用dp[i][j][p][k] 表示i到j的区间，左端点是什么颜色，右端点是什么颜色。用DFS实现比较简单一点，用递推很烦

关于区间DP,可以参照这个博客

http://blog.csdn.net/dacc123/article/details/50885903

#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <algorithm>
#include <math.h>
#include <stdio.h>
#include <stack>

using namespace std;
const long long int mod=1e9+7;
char a[705];
long long int dp[705][705][3][3];
int s[705];
int m[705];
int top;
void dfs(int i,int j)
{
     if(j-i==1)
     {
        dp[i][j][0][1]=1;
        dp[i][j][0][2]=1;
        dp[i][j][1][0]=1;
        dp[i][j][2][0]=1;
        return;
     }
      else if(m[i]==j)
     {
         dfs(i+1,j-1);
        for(int p=0;p<3;p++)
        {
            for(int q=0;q<3;q++)
            {
                if(q!=1) dp[i][j][0][1]=(dp[i][j][0][1]+dp[i+1][j-1][p][q])%mod;
                if(q!=2) dp[i][j][0][2]=(dp[i][j][0][2]+dp[i+1][j-1][p][q])%mod;
                if(p!=1) dp[i][j][1][0]=(dp[i][j][1][0]+dp[i+1][j-1][p][q])%mod;
                if(p!=2) dp[i][j][2][0]=(dp[i][j][2][0]+dp[i+1][j-1][p][q])%mod;
            }
        }
        return;
     }
     else
     {
         int k=m[i];
         dfs(i,k);
         dfs(k+1,j);
         for(int p=0;p<3;p++)
            for(int q=0;q<3;q++)
               for(int x=0;x<3;x++)
                  for(int y=0;y<3;y++)
                     if(!((y==1&&x==1)||(y==2&&x==2)))
                        dp[i][j][p][q]=(dp[i][j][p][q]+(dp[i][k][p][x]*dp[k+1][j][y][q])%mod)%mod;
         return;
     }

}
int main()
{
    while(scanf("%s",a)!=EOF)
    {
        int len=strlen(a);
        top=-1;
        for(int i=0;i<len;i++)
        {
            if(a[i]=='(')

                s[++top]=i;
            else
            {
                m[s[top]]=i;
				//m[i]=s[top];
                top--;
            }
        }
        memset(dp,0,sizeof(dp));
        dfs(0,len-1);
        long long int ans=0;
        for(int i=0;i<3;i++)
            for(int j=0;j<3;j++)
                 ans=(ans+dp[0][len-1][i][j])%mod;
        printf("%lld\n",ans);
    }
    return 0;
}