用Python深入理解跳跃表原理及实现

最近看 Redis 的实现原理，其中讲到 Redis 中的有序数据结构是通过跳跃表来进行实现的。第一次听说跳跃表的概念，感到比较新奇，所以查了不少资料。其中，网上有部分文章是按照如下方式描述跳跃表的：

这种描述便于理解，很容易让人理解到跳跃表是建立了类似索引的东西，从而提高效率的。但是，这样描述给人的感觉是，数据有多份存储，每份数据有两个指针，指向下层数据的指针和指向右面数据的指针。然而实际并不是这样的，实际的数据结构如下：

即：并非由多份数据，而是每份数据有多层指针。

那么，什么是跳跃表，跳跃表有什么特点呢？

• Skip lists are data structures that use probabilistic balancing rather than strictly enforced balancing. As a result, the algorithms for insertion and deletion in skip lists are much simpler and significantly faster than equivalent algorithms for balanced trees.

从定义中可以看出，跳跃表是为了解决平衡树插入或者删除操作过于复杂而进行设计的。的确，平衡树在插入或者删除时，需要维持平衡而进行过多的操作，学过数据结构的同学想到平衡树、红黑树等都不寒而栗吧。而跳跃表则没有这种问题，采用了随机的思想简化了维持平衡的过程，而保持查找的时间复杂度依旧是O(log N)。

跳跃表有如下特点：

(1) 每个跳跃表由很多层结构组成；

(2) 每一层都是一个有序链表，且第一个节点是头节点；

(3) 最底层的有序链表包含所有节点；

(4) 每个节点可能有多个指针，这与节点所包含的层数有关；

(5) 跳跃表的查找、插入、删除的时间复杂度均为O(log N)。

从上面的结构也可以看出，跳跃表的核心思想就是，每一个节点既包含指向下一个节点的指针，也可能包含很多个指向后续节点的指针，这样在查找、插入、删除某个节点的过程中，可以避免一些不必要的节点，从而提高效率。

所以，每个节点的数据结构设计如下：

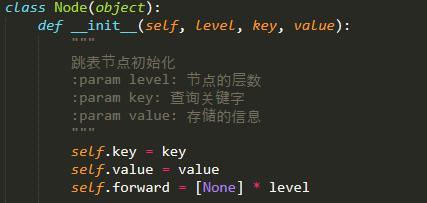
跳跃表的设计如下：

那么，如何进行查找呢？

假设查找5，那么在查找的过程中，需要从最高层开始查找（毕竟，越高层越表示索引嘛，很可能一下子就找到数据了），如果元素小于5，则一直向右查找。若遇到大于5的，则降低一层，在下一层继续查找。查找的流程如下图所示：

查找的代码如下：

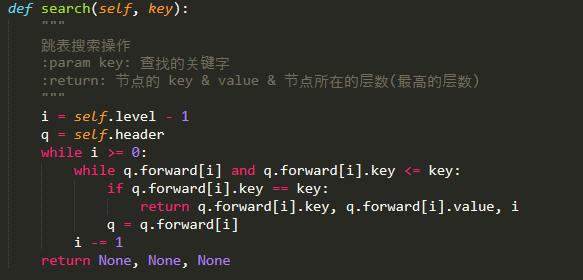
插入的过程是怎么样的呢？

插入的过程包括如下4个步骤：

1、首先，需要找到每一层要插入节点的位置，并保存（用于后续调整指针）；

2、确定该节点包含的层数，初始化要插入的节点；

3、相关的指针的调整；

4、若跳跃表层数增加，需要调整Header节点。

如下图，若要插入key 为4.5的节点，先要找到需要插入的位置，如图中黄线所示，然后随机生成一个层数（范围是1层到当前跳跃表层数+1，随机数生成器可以自行设计），初始化该节点，然后进行调整指针。

假设随机生成的层数为3，那么插入后为：

是不是比平衡树简单多了？当然，如果随机生成的层数为 当前跳跃表层数+1，那么跳跃表层数增加一层，header节点需要增加一层。

Python实现如下：

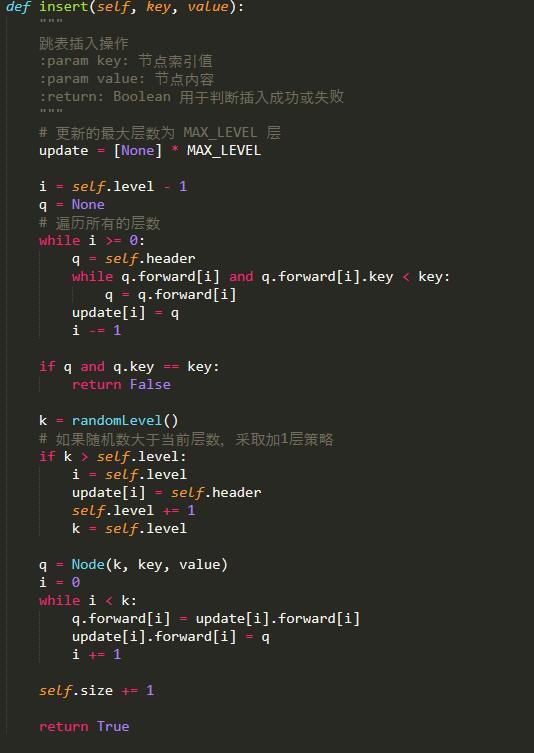
删除操作呢？跟插入操作类似，但是更为简单，只需要如下3个步骤：

1、首先，需要找到每一层要删除节点的位置，并保存（用于后续调整指针）；

2、相关的指针的调整；

3、若层数减少，需要调整跳跃表层数和Header节点。

如果删除6这个节点，找到相应的位置，然后调整指针即可：

删除后的结果为：

Python代码实现为：

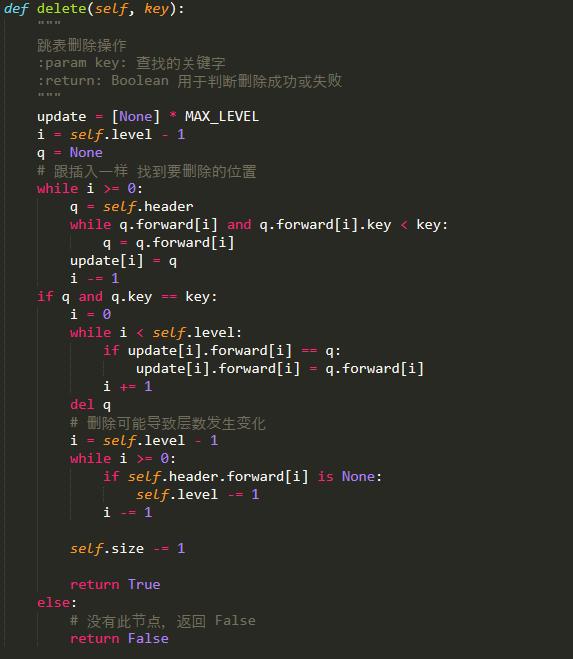
这里需要注意，如果删除元素后导致层数发生变化，那么需要对header节点进行调整的，即降低一层。

跳跃表的原理及实现你是否深入理解了？