6-16 Topological Sort（25 分）

Write a program to find the topological order in a digraph.

Format of functions:

bool TopSort( LGraph Graph, Vertex TopOrder[] );

where LGraph is defined as the following:

typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{
    Vertex AdjV;
    PtrToAdjVNode Next;
};

typedef struct Vnode{
    PtrToAdjVNode FirstEdge;
} AdjList[MaxVertexNum];

typedef struct GNode *PtrToGNode;
struct GNode{
    int Nv;
    int Ne;
    AdjList G;
};
typedef PtrToGNode LGraph;

The topological order is supposed to be stored in TopOrder[] where TopOrder[i] is the i-th vertex in the resulting sequence. The topological sort cannot be successful if there is a cycle in the graph -- in that case TopSort must return false; otherwise return true.

Notice that the topological order might not be unique, but the judge's input guarantees the uniqueness of the result.

Sample program of judge:

#include <stdio.h>
#include <stdlib.h>

typedef enum {false, true} bool;
#define MaxVertexNum 10  /* maximum number of vertices */
typedef int Vertex;      /* vertices are numbered from 0 to MaxVertexNum-1 */

typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{
    Vertex AdjV;
    PtrToAdjVNode Next;
};

typedef struct Vnode{
    PtrToAdjVNode FirstEdge;
} AdjList[MaxVertexNum];

typedef struct GNode *PtrToGNode;
struct GNode{
    int Nv;
    int Ne;
    AdjList G;
};
typedef PtrToGNode LGraph;

LGraph ReadG(); /* details omitted */

bool TopSort( LGraph Graph, Vertex TopOrder[] );

int main()
{
    int i;
    Vertex TopOrder[MaxVertexNum];
    LGraph G = ReadG();

    if ( TopSort(G, TopOrder)==true )
        for ( i=0; i<G->Nv; i++ )
            printf("%d ", TopOrder[i]);
    else
        printf("ERROR");
    printf("\n");

    return 0;
}

/* Your function will be put here */

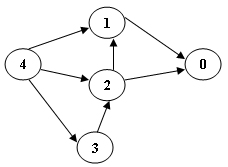
Sample Input 1 (for the graph shown in the figure):

5 7
1 0
4 3
2 1
2 0
3 2
4 1
4 2

Sample Output 1:

4 3 2 1 0

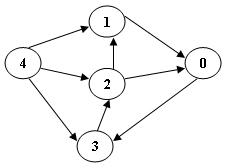
Sample Input 2 (for the graph shown in the figure):

5 8
0 3
1 0
4 3
2 1
2 0
3 2
4 1
4 2

Sample Output 2:

ERROR

代码：

 

bool TopSort( LGraph Graph, Vertex TopOrder[] )
{
    int c = ;
    int book[Graph -> Nv],h[Graph -> Nv + ],head = ,tail = ;
    PtrToAdjVNode t;
    for(int i = ;i < Graph -> Nv;i ++)
        book[i] = ;
    for(int i = ;i < Graph -> Nv;i ++)
    {
        t = Graph -> G[i].FirstEdge;
        while(t)
        {
            book[t -> AdjV] ++;
            t = t -> Next;
        }
    }
    for(int i = ;i < Graph -> Nv;i ++)
    {
        if(book[i] == )
        {
            h[tail ++] = i;
        }
    }
    if(head == tail)return false;
    while(head < tail)
    {
        t = Graph -> G[h[head]].FirstEdge;
        while(t)
        {
            if(book[t -> AdjV] <= )return false;
            book[t -> AdjV] --;
            if(book[t -> AdjV] == )h[tail ++] = t -> AdjV;
            t = t -> Next;
        }
        book[h[head]] = -;
        TopOrder[c ++] = h[head ++];
    }
    if(c != Graph -> Nv)return false;///有回路
    return true;
}