LDA的Gibbs Sampling求解
《LDA数学八卦》对于LDA的Gibbs Sampling求解讲得很详细,在此不在重复在轮子,直接贴上该文这部分内容。
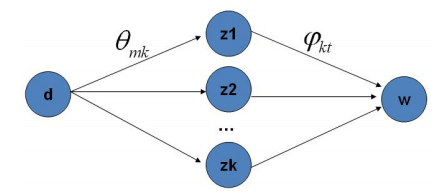
Gibbs Sampling



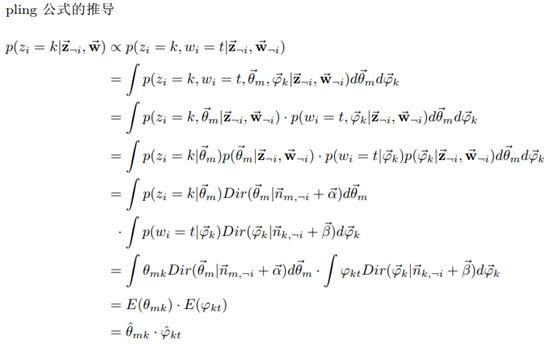
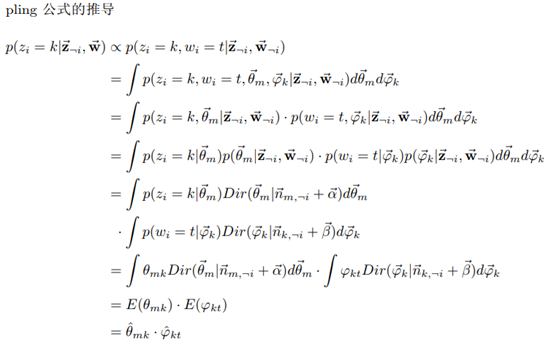
批注:
1、 对于第i个词语,上式k(主题类型)未知,取值范围为[1, K],t(词语类型)已知,即观测值。
2、 由于doc-topic与topic-word独立,所以第i个词语主题为k,类型为t的概率显然是主题k概率在doc m-topic分布上的积分乘以词语t概率在topic k-word分布上的积分。即 。
。

批注:我们已经得到了每个topic-word的边缘分布,通过Gibbs Sampling很容易得到topic-word的完整分布。
Training And Inference



LDA的Gibbs Sampling求解的更多相关文章
- 随机采样和随机模拟:吉布斯采样Gibbs Sampling实现文档分类
http://blog.csdn.net/pipisorry/article/details/51525308 吉布斯采样的实现问题 本文主要说明如何通过吉布斯采样进行文档分类(聚类),当然更复杂的实 ...
- LDA Gibbs Sampling
注意:$\alpha$和$\beta$已知,常用为(和LDA EM算法不同) 1. 为什么可用 LDA模型求解的目标为得到$\phi$和$\theta$ 假设现在已知每个单词对应的主题$z$,则可 ...
- 深度学习方法:受限玻尔兹曼机RBM(三)模型求解,Gibbs sampling
欢迎转载,转载请注明:本文出自Bin的专栏blog.csdn.net/xbinworld. 技术交流QQ群:433250724,欢迎对算法.技术.应用感兴趣的同学加入. 接下来重点讲一下RBM模型求解 ...
- 随机采样和随机模拟:吉布斯采样Gibbs Sampling
http://blog.csdn.net/pipisorry/article/details/51373090 吉布斯采样算法详解 为什么要用吉布斯采样 通俗解释一下什么是sampling. samp ...
- PRML读书会第十一章 Sampling Methods(MCMC, Markov Chain Monte Carlo,细致平稳条件,Metropolis-Hastings,Gibbs Sampling,Slice Sampling,Hamiltonian MCMC)
主讲人 网络上的尼采 (新浪微博: @Nietzsche_复杂网络机器学习) 网络上的尼采(813394698) 9:05:00 今天的主要内容:Markov Chain Monte Carlo,M ...
- Gibbs Sampling深入理解
二维Gibbs Sampling算法 Gibbs Sampling是高维概率分布的MCMC采样方法.二维场景下,状态(x, y)转移到(x’, y’),可以分为三种场景 (1)平行于y轴转移,如上图中 ...
- 关于LDA的gibbs采样,为什么可以获得正确的样本?
算法里面是随机初始了一个分布,然后进行采样,然后根据每次采样的结果去更新分布,之后接着采样直到收敛. 1.首先明确一下MCMC方法. 当我们面对一个未知或者复杂的分布时,我们经常使用MCMC方法来进行 ...
- 随机采样方法整理与讲解(MCMC、Gibbs Sampling等)
本文是对参考资料中多篇关于sampling的内容进行总结+搬运,方便以后自己翻阅.其实参考资料中的资料写的比我好,大家可以看一下!好东西多分享!PRML的第11章也是sampling,有时间后面写到P ...
- LDA-math-MCMC 和 Gibbs Sampling
http://cos.name/2013/01/lda-math-mcmc-and-gibbs-sampling/ 3.1 随机模拟 随机模拟(或者统计模拟)方法有一个很酷的别名是蒙特卡罗方法(Mon ...
随机推荐
- 使用IntelliJ IDEA创建Maven聚合工程、创建resources文件夹、ssm框架整合、项目运行一体化
一.创建一个空的项目作为存放整个项目的路径 1.选择 File——>new——>Project ——>Empty Project 2.WorkspaceforTest为项目存放文件夹 ...
- 自然语言处理nlp工具
1.结巴 适合语言:python 应用场景:中文分词较好 不适用于命名实体识别.信息抽取 2.nltk 适合语言:python 应用场景:不适用于中文分词,效果较差 提供了一些用于方便的方法
- finecms5采集接口下载
哪里有finecms采集接口可以下载?我们在用finecms建站时比较纠结的是要如何采集文章,finecms商城是有售卖采集插件,价格是50元,有些朋友感觉比较贵,不太愿意买,我们也是比较权衡了才很久 ...
- 并发编程---死锁||递归锁---信号量---Event事件---定时器
死锁 互斥锁:Lock(),互斥锁只能acquire一次 递归锁: RLock(),可以连续acquire多次,每acquire一次计数器+1,只有计数为0时,才能被抢到acquire # 死锁 f ...
- 永久有效的 webstorm license server 20180808
下载地址 https://download.jetbrains.com/webstorm/WebStorm-2018.3.2.exe 2018年10月26日,最近老是过期,搞了一个1年有效的代码,是 ...
- abap异常处理 , update module
1:异常 https://www.cnblogs.com/rainysblog/p/6665455.html 2:update module https://www.cnblogs.com/cindy ...
- get请求乱码解决
1.修改tomcat的配置文件 <ConnectorURIEncoding="utf-8" connectionTimeout="20000" port= ...
- Python 全栈开发一 python初识
1.Python简介 python的创始人为吉多·范罗苏姆(Guido van Rossum).1989年的圣诞节期间,吉多·范罗苏姆为了在阿姆斯特丹打发时间,决心开发一个新的脚本解释程序,作为ABC ...
- 10.26 配置psplkf小程序
环境 服务器 Win Server 2008,nginx, maven, psplkf 标准的mvn工程,可以使用eclipse,导入,file-import-maven project就行, 但是我 ...
- 模块讲解----pickle模块(只在python用的序列化与反序列化)
特点 1.只能在python中使用,只支持python的基本数据类型. 2.可以处理复杂的序列化语法.(例如自定义的类的方法,游戏的存档等) 3.序列化的时候,只是序列化了整个序列对象,而不是内存地址 ...
