CCPC-Wannafly Winter Camp Day5 Div1 - Sorting - [线段树]

题目链接：https://zhixincode.com/contest/22/problem/I?problem_id=314

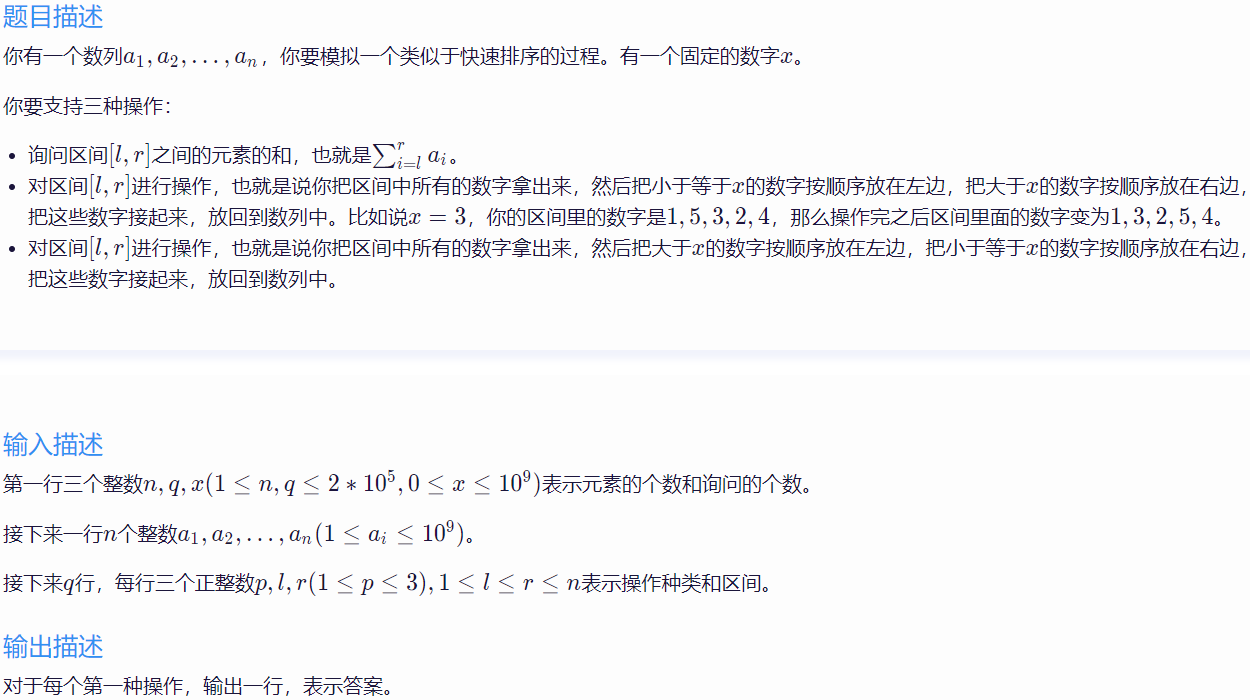
样例输入 1

5 9 3
1 5 3 2 4
1 1 5
2 1 5
1 1 1
1 2 2
1 3 3
1 4 4
1 5 5
3 3 5
1 1 4

样例输出 1

15
1
3
2
5
4
13

题解：

dls出的题真好qwq！

我们先考虑partition的两种操作，若将所有小于等于 $x$ 的数字看成 $0$，将所有大于 $x$ 的数字看成 $1$，那么原序列就变成了一个 $01$ 序列。

那么两种partition操作，就相当于将某个区间内的所有 $0$ 放到一边，所有 $1$ 放到另一边。这个操作就很简单，我们可以 $O(\log n)$ 统计出该区间内有多少个 $0$ 以及多少个 $1$，然后相应的将区间的左边一段赋值成 $0$（或者 $1$），将区间右边一段赋值成 $1$（或者 $0$）。

然后，对于求和操作：

首先不难发现，不管怎么操作，对于所有小于等于 $x$ 的数字来说，它们之间的顺序是不会改变的；同样对于所有大于 $x$ 的数字，它们之间的顺序也不会改变。因此，对于任意一个位置，假设该位置上是一个 $0$，那么只要统计这个位置左侧有几个 $0$ 就可以知道，这个位置对应到原序列是什么数字。当然，我们若是对区间内每个位置都这样去求出是多少，再求和，显然时间复杂度是比较差的。

因此，我们可以根据前缀和的思想，对于要求和的区间 $[l,r]$，我们可以 $O(\log n)$ 统计出 $[1,l-1]$ 和 $[1,r]$ 各有多少个 $0$，然后我们就知道了 $[l,r]$ 区间对应到原序列是哪个区间，然后原序列做一下前缀和求差值即可得到答案。类似的，统计 $1$ 的数目也是这样一个道理。

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=2e5+;

int n,q,x,v[maxn];
int tota,totb;
ll a[maxn],b[maxn];

#define ls (rt<<1)
#define rs (rt<<1|1)
struct Node{
    int l,r;
    int val,lazy;
    void update(int x)
    {
        val=(r-l+)*x;
        lazy=x;
    }
}o[maxn<<];
void pushdown(int rt)
{
    if(o[rt].lazy==-) return;
    o[ls].update(o[rt].lazy);
    o[rs].update(o[rt].lazy);
    o[rt].lazy=-;
}
inline void pushup(int rt)
{
    o[rt].val=o[ls].val+o[rs].val;
}
void build(int rt,int l,int r)
{
    o[rt].l=l, o[rt].r=r;
    o[rt].lazy=-;
    if(l==r)
    {
        o[rt].val=(v[l]>x);
        return;
    }
    int mid=(l+r)>>;
    build(ls,l,mid);
    build(rs,mid+,r);
    pushup(rt);
}
void update(int rt,int st,int ed,int val)
{
    if(st<=o[rt].l && o[rt].r<=ed)
    {
        o[rt].update(val);
        return;
    }
    pushdown(rt);
    int mid=(o[rt].l+o[rt].r)>>;
    if(st<=mid) update(ls,st,ed,val);
    if(mid<ed) update(rs,st,ed,val);
    pushup(rt);
}
int query(int rt,int st,int ed)
{
    if(st>ed) return ;
    if(st<=o[rt].l && o[rt].r<=ed) return o[rt].val;
    pushdown(rt);
    int mid=(o[rt].l+o[rt].r)>>, res=;
    if(st<=mid) res+=query(ls,st,ed);
    if(mid<ed) res+=query(rs,st,ed);
    pushup(rt);
    return res;
}

int main()
{
    ios::sync_with_stdio();
    cin.tie(), cout.tie();

    cin>>n>>q>>x;

    tota=totb=, a[]=b[]=;
    for(int i=;i<=n;i++)
    {
        cin>>v[i];

        //按x拆分序列并求前缀和
        if(v[i]<=x) a[++tota]=a[tota-]+v[i];
        if(v[i]>x) b[++totb]=b[totb-]+v[i];
    }

    build(,,n);
    while(q--)
    {
        int t,l,r; cin>>t>>l>>r;
        if(t==)
        {
            int r_cnt1=query(,,r), r_cnt0=(r-+)-r_cnt1;
            int l_cnt1=query(,,l-), l_cnt0=((l-)-+)-l_cnt1;
            cout<<(a[r_cnt0]-a[l_cnt0])+(b[r_cnt1]-b[l_cnt1])<<'\n';
        }
        if(t==)
        {
            int cnt1=query(,l,r), cnt0=(r-l+)-cnt1;
            update(,l,l+cnt0-,), update(,r-cnt1+,r,);
        }
        if(t==)
        {
            int cnt1=query(,l,r), cnt0=(r-l+)-cnt1;
            update(,l,l+cnt1-,), update(,r-cnt0+,r,);
        }
    }
}