[Machine Learning] logistic函数和softmax函数

　　简单总结一下机器学习最常见的两个函数，一个是logistic函数，另一个是softmax函数，若有不足之处，希望大家可以帮忙指正。本文首先分别介绍logistic函数和softmax函数的定义和应用，然后针对两者的联系和区别进行了总结。

1. logistic函数

1.1 logistic函数定义

　　引用wiki百科的定义：

　　A logistic function or logistic curve is a common "S" shape (sigmoid curve).

　　其实逻辑斯谛函数也就是经常说的sigmoid函数，它的几何形状也就是一条sigmoid曲线。

　　logistic函数的公式形式如下：

$f(x) = \frac{L}{1+e^{-k(x-x_{0})}}$

　　其中，$x_{0}$表示了函数曲线的中心（sigmoid midpoint），$k$是曲线的坡度。

　　logistic的几何形状如下所示：

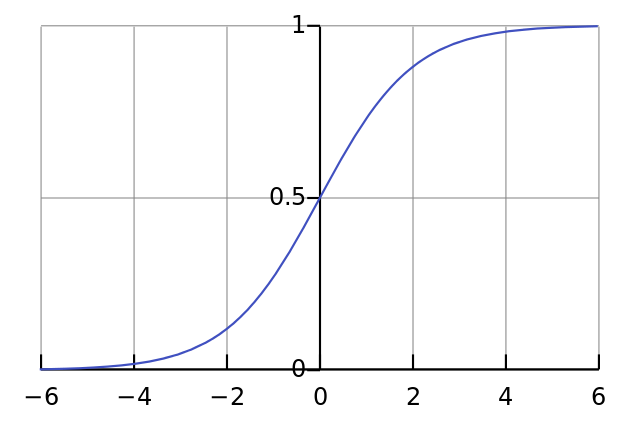
1.2 logistic函数的应用

　　logistic函数本身在众多领域中都有很多应用，我们只谈统计学和机器学习领域。

　　logistic函数在统计学和机器学习领域应用最为广泛或者最为人熟知的肯定是逻辑斯谛回归模型了。逻辑斯谛回归（Logistic Regression，简称LR）作为一种对数线性模型（log-linear model）被广泛地应用于分类和回归场景中。此外，logistic函数也是神经网络最为常用的激活函数，即sigmoid函数。

2. softmax函数

2.1 softmax函数的定义

　　同样，我们贴一下wiki百科对softmax函数的定义：

　　softmax is a generalization of logistic function that "squashes"(maps) a $K$-dimensional vector $z$ of arbitrary real values to a $K$-dimensional vector $\sigma(z)$ of real values in the range (0, 1) that add up to 1.

　　这句话既表明了softmax函数与logistic函数的关系，也同时阐述了softmax函数的本质就是将一个$K$维的任意实数向量压缩（映射）成另一个$K$维的实数向量，其中向量中的每个元素取值都介于（0，1）之间。

　　softmax函数形式如下：

$\sigma(z)_{j}=\frac{e^{z_{j}}}{\sum^{K}_{k=1}e^{z_{k}}}$

　　其中$j = 1,2, ... , K$。

2.2 sotfmax函数的应用

　　softmax函数经常用在神经网络的最后一层，作为输出层，进行多分类。此外，softmax在增强学习领域内，softmax经常被用作将某个值转化为激活概率，这类情况下，softmax的公式如下：

$P_{t}(a)=\frac{e^{\frac{q_{t}(a)}{T}}}{\sum^{n}_{i=1}e^{\frac{q_{t}(i)}{T}}}$

　　其中，$T$被称为是温度参数（temperature parameter）。当T很大时，即趋于正无穷时，所有的激活值对应的激活概率趋近于相同（激活概率差异性较小）；而当T很低时，即趋于0时，不同的激活值对应的激活概率差异也就越大。这个结论很重要，Hinton在2015年的一篇paper中重点阐释了如何根据温度参数来soften神经网络的输出，从而提出了distillation的思想和方法。

3. logistic和softmax的关系

　　1）logistic具体针对的是二分类问题，而softmax解决的是多分类问题，因此从这个角度也可以理解logistic函数是softmax函数的一个特例。

　　这里借鉴UFLDL教程中的推导，具体的推导过程如下：

　　当分类数为2时，softmax回归的假设函数表示如下：

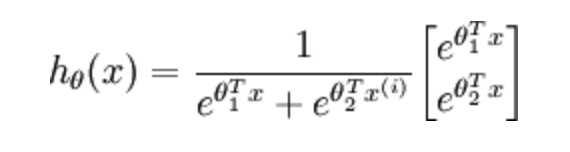
　　利用softmax回归参数冗余的特点，从两个参数向量中都减去向量$\theta_{1}$，得到：

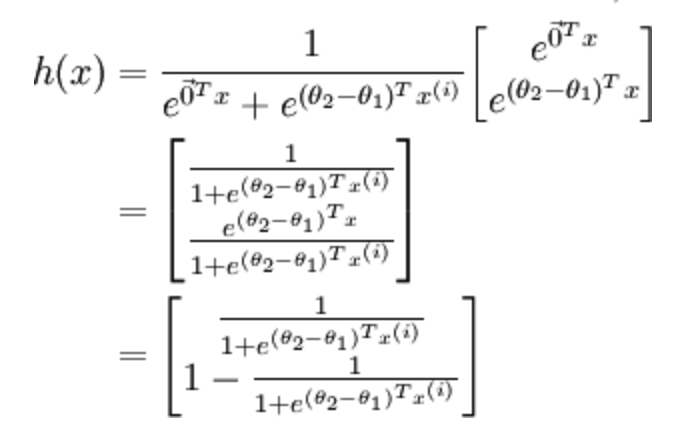
　　最后，用$\theta^{'}$来表示$\theta_{2}-\theta_{1}$，上述公式可以表示为softmax回归器预测其中一个类别的概率为

$\frac{1}{1+e^{\theta^{'T}x^{i}}}$

　　另一个类别的概率为

$1-\frac{1}{1+e^{\theta^{'T}x^{i}}}$

　　这与logistic回归是完全一致的。

　　2）从概率角度来看logistic和softmax函数的区别。

　　softmax建模使用的分布是多项式分布，而logistic则基于伯努利分布，这方面具体的解释可以参考Andrew Ng的讲义去理解。

　　3）softmax回归和多个logistic回归的关系。

　　有了解的同学可能知道多个logistic回归通过叠加也同样可以实现多分类的效果，那么多个logistic回归和softmax一样不一样呢？

　　softmax回归进行的多分类，类与类之间是互斥的，即一个输入只能被归为一类；

　　多个logistic回归进行多分类，输出的类别并不是互斥的，即"苹果"这个词语既属于"水果"类也属于"3C"类别。

4. 参考内容

　　[1] wiki百科：logistic函数

　　[2] wiki百科：softmax函数

　　[3] UFLDL教程之softmax回归