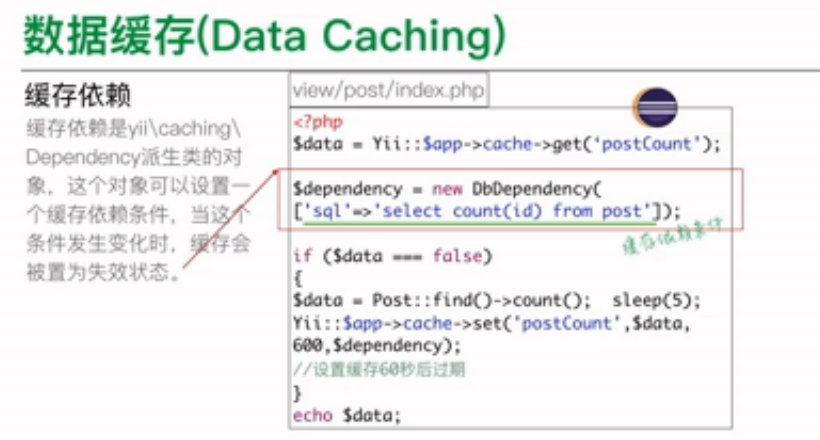
Yii2缓存依赖

Yii2缓存依赖的更多相关文章
- 如何使用yii2的缓存依赖特性
目录 如何使用yii2的缓存依赖特性 概述 页面缓存 缓存依赖 链式依赖 总结 如何使用yii2的缓存依赖特性 概述 缓存是Yii2的强大特性之一,合理使用缓存技术可以有效地减小服务器的访问压力.Yi ...
- Yii2.0数据库缓存依赖发布的使用理解
对于产品中经常需要生成一些缓存类的东西,比如系统基础配置,商品分类等,每次修改调整后都要手动进行缓存发布,是不是非常麻烦!这时候Yii2.0的缓存依赖发布就起到至关重要的作用了!现将主要的使用流程介绍 ...
- YII2数据库依赖缓存
首先配置一下缓存,自己选择是用文件缓存还是数据库缓存等. 'cache' => [ 'class' => 'yii\caching\FileCache', ], 然后就可以通过 Yii:: ...
- 缓存技术之——Yii2性能优化之:缓存依赖
Yii中的缓存依赖,简单来说就是将缓存和另外一个东西绑定在一起,如果另外一个东西发生变化,那么缓存也将发生变化.有点儿类似于JS中的触发事件(但是也不那么像),缓存的变动是依赖的东西所导致的. 依赖可 ...
- Yii2.0 依赖注入(DI)和依赖注入容器的原理
依赖注入和依赖注入容器 为了降低代码耦合程度,提高项目的可维护性,Yii采用多许多当下最流行又相对成熟的设计模式,包括了依赖注入(Denpdency Injection, DI)和服务定位器(Serv ...
- 缓存依赖中cachedependency对象
缓存依赖主要提供以下功能:1.SQL 缓存依赖项可用于应用程序缓存和页输出缓存.2.可在 SQL Server 7.0 及更高版本中使用 SQL 缓存依赖项.3.可以在网络园(一台服务器上存在多个处理 ...
- SQL server数据缓存依赖
SQL server数据缓存依赖有两种实现模式,轮询模式,通知模式. 1 轮询模式实现步骤 此模式需要SQL SERVER 7.0/2000/2005版本以上版本都支持 主要包含以下几 ...
- ASP.NET MVC3系列页面缓存、缓存依赖SQL(真实项目注意细节)
缓存依赖数据库 第一步 1通过vs里面带的命令提示窗口. 2或者.NET Framework 版本 4(64 位系统)条件,%windir%\Microsoft.NET\Framework64\v4. ...
- cache应用(asp.net 2.0 SQL数据缓存依赖 [SqlCacheDependency ] )
Asp.net 2.0 提供了一个新的数据缓存功能,就是利用sql server2005 的异步通知功能来实现缓存 1.首先在sqlserver2005 中创建一个test的数据库. 在SQL Ser ...
随机推荐
- 2018/04/14 理解oAuth2.0
最近都近没有更新博客了,卡在 oAuth 上了. 之前公司做统一身份的认证,不了解 oAuth 的我在这卡了两天. 于是决定仔细研究原理,理论指导实践. -- 什么是 oAuth ? 简单来说 oAu ...
- select下拉菜单实现通过数据库查询来设置默认值
查询网上各种资料要不比较难理解,要么有问题,现有一种简单通俗的理解方法 思路:读取数据库数据1,数据2需用到select选择菜单,但是又想每次查看是都显示读数据库的默认信息 demo: {% for ...
- Linux snprintf使用总结
snprintf()函数用于将格式化的数据写入字符串,其原型为: int snprintf(char *str, int n, char * format [, argument, ...]); ...
- bug: '\xff' 转换成-1 而不是255
后台给的值处理后 Byte rtncode = payload[0]; 打印payload[0]是'\xff', 增加 if (rtncode ==255 ){ ....} 的判断,跳里面去了 然后用 ...
- 自定义指令(v-check、v-focus)的方法有哪些?它有哪些钩子函数?还有哪些钩子函数参数?
全局定义指令:在vue对象的directive方法里面有两个参数,一个是指令名称,另一个是函数.组件内定义指令:directives: 钩子函数:bind(绑定事件触发).inserted(节点插入的 ...
- 浏览器的兼容性(CSS浏览器兼容性、CSS hack)
一.关于CSS hack(尽量不用或者少用,减少页面复杂度) 1.条件注释法:(我的测试是IE9及其以下才有效) 这种方式是IE浏览器专有的Hack方式,微软官方推荐使用的hack方式.举例如下 只在 ...
- 用canvas画三角形的方法
<canvas id="favoriteRectangle" width="30" height="30"></canva ...
- 腾讯互动课堂(Tencent Interact Class,TIC)SDK 词汇表
词汇表 https://cloud.tencent.com/document/product/266/11732 封装格式 封装格式(Format)是将已经编码压缩好的视频流和音频流按照一定的格式规范 ...
- IIS下实现帝国CMS搜索页伪静态
前面ytkah讲了apache下帝国CMS搜索页伪静态实现方法,网友说服务器是用IIS,那么IIS下如何实现帝国CMS搜索页伪静态呢?首先得先有URL重写插件,下载地址:http://www.iis. ...
- 20170803 Airflow自带的API进行GET 和POST动作部分内容
--1 首先你要有安装好的Airflow 环境并且在配置文件中有启用API 属性 --2 就是GET 和POST 方法的调用了 这里说一下,由于Airflow在网络上的资料比较少,可以从GETHUB中 ...
