HanLP二元核心词典详细解析

本文分析：HanLP版本1.5.3中二元核心词典的存储与查找。当词典文件没有被缓存时，会从文本文件CoreNatureDictionary.ngram.txt中解析出来存储到TreeMap中，然后构造start和pair数组，并基于这两个数组实现词共现频率的二分查找。当已经有缓存bin文件时，那直接读取构建start和pair数组，速度超快。

源码实现

二元核心词典的加载

二元核心词典在文件：CoreNatureDictionary.ngram.txt，约有46.3 MB。程序启动时先尝试加载CoreNatureDictionary.ngram.txt.table.bin 缓存文件，大约22.9 MB。这个缓存文件是序列化保存起来的。

ObjectInputStream in = new ObjectInputStream(IOUtil.newInputStream(path));

start = (int[]) in.readObject();

pair = (int[]) in.readObject();

当缓存文件不存在时，抛出异常：警告: 尝试载入缓存文件E:/idea/hanlp/HanLP/data/dictionary/CoreNatureDictionary.ngram.txt.table.bin发生异常[java.io.FileNotFoundException: 然后解析CoreNatureDictionary.ngram.txt

br = new BufferedReader(new InputStreamReader(IOUtil.newInputStream(path), "UTF-8"));

while ((line = br.readLine()) != null){

String[] params = line.split("\\s");

String[] twoWord = params[0].split("@", 2);

...

}

然后，使用一个TreeMap<Integer, TreeMap<Integer, Integer>> map来保存解析的每一行二元核心词典条目。

TreeMap<Integer, TreeMap<Integer, Integer>> map = new TreeMap<Integer, TreeMap<Integer, Integer>>();

int idA = CoreDictionary.trie.exactMatchSearch(a);//二元接续的 @ 前的内容

int idB = CoreDictionary.trie.exactMatchSearch(b);//@ 后的内容

TreeMap<Integer, Integer> biMap = map.get(idA);

if (biMap == null){

biMap = new TreeMap<Integer, Integer>();

map.put(idA, biMap);//

}

biMap.put(idB, freq);

比如二元接续：“一 一@中”，@ 前的内容是：“一 一”，@后的内容是 “中”。由于同一个前缀可以有多个后续，比如：

一一@中 1

一一@为 6

一一@交谈 1

所有以 '一 一' 开头的 @ 后的后缀 以及对应的频率 都保存到 相应的biMap中：biMap.put(idB, freq);。注意：biMap和map是不同的，map保存整个二元核心词典，而biMap保存某个词对应的所有后缀(这个词 @ 后的所有条目)

map中保存二元核心词典示意图如下：

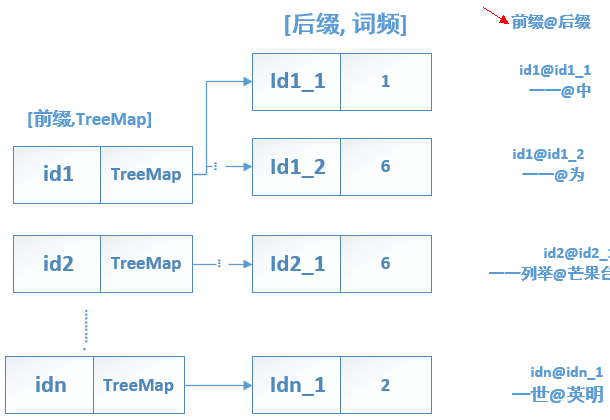
二元核心词典主要由CoreBiGramTableDictionary.java 实现。这个类中有两个整型数组 支撑 二元核心词典的快速二分查找。

/**

* 描述了词在pair中的范围，具体说来<br>

* 给定一个词idA，从pair[start[idA]]开始的start[idA + 1] - start[idA]描述了一些接续的频次

*/

static int start[];//支持快速地二分查找

/**

* pair[偶数n]表示key，pair[n+1]表示frequency

*/

static int pair[];

start 数组

首先初始化一个与一元核心词典Trie树 size 一样大小 的start 数组：

int maxWordId = CoreDictionary.trie.size();

...

start = new int[maxWordId + 1];

然后，遍历一元核心词典中的词，寻找这些词是 是否有二阶共现（或者说：这些词是否存在 二元接续）

for (int i = 0; i < maxWordId; ++i){

TreeMap<Integer, Integer> bMap = map.get(i);

if (bMap != null){

for (Map.Entry<Integer, Integer> entry : bMap.entrySet()){

//省略其他代码

++offset;//统计以 这个词 为前缀的所有二阶共现的个数

}

}//end if

start[i + 1] = offset;

}// end outer for loop

if (bMap != null)表示 第 i 个词(i从下标0开始)在二元词典中有二阶共现，于是 统计以 这个词 为前缀的所有二阶共现的个数，将之保存到 start 数组中。下面来具体举例，start数组中前37个词的值如下：

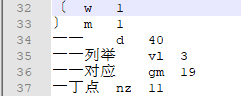
其中start[32]=0，start[33]=0，相应的 一元核心词典中的词为 （ ）。即，一个左括号、一个右括号。而这个 左括号 和 右括号 在二元核心词典中是不存在词共现的(接续)。也就是说在二元核心词典中 没有 （@xxx这样的条目，也没有 )@xxx 这个条目(xxx 表示任意以 ( 或者 ) 为前缀 的后缀接续)。因此，这也是start[32] 和 start[33]=0 都等于0的原因。

部分词的一元核心词典如下：

再来看 start[34]=22，start[35]=23。在一元核心词典中，第34个词是"一 一"，而在二元核心词典中 '一 一'的词共现共有22个，如下：

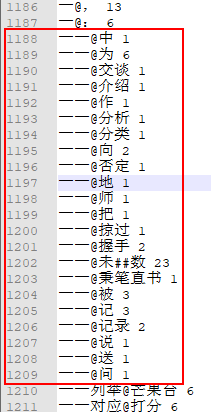
在一元核心词典中，第35个词是 "一 一列举"，如上图所示，"一 一列举" 在二元核心中只有一个词共现：“一 一列举@芒果台”。因此，start[35]=22+1=23。从这里也可以看出：

给定一个词idA，从pair[start[idA]]开始的start[idA + 1] - start[idA]描述了一些接续的频次

比如，idA=35，对应词“一 一列举”，它的接续频次为1，即：23-22=1

这样做的好处是什么呢？自问自答一下：^~^，就是大大减少了二分查找的范围。

pair 数组

pair数组的长度是二元核心词典行数的两倍

int total = 0;

while ((line = br.readLine()) != null){

//省略其他代码

total += 2;

}

pair数组 偶数 下标 存储 保存的是 一元核心词典中的词 的下标，而对应的偶数加1 处的下标 存储 这个词的共现频率。即： pair[偶数n]表示key，pair[n+1]表示frequency

pair = new int[total];  // total是接续的个数*2

for (int i = 0; i < maxWordId; ++i)

{

TreeMap<Integer, Integer> bMap = map.get(i);//i==0?

if (bMap != null)//某个词在一元核心词典中, 但是并没有出现在二元核心词典中(这个词没有二元核心词共现)

{

for (Map.Entry<Integer, Integer> entry : bMap.entrySet())

{

int index = offset << 1;

pair[index] = entry.getKey();//词 在一元核心词典中的id

pair[index + 1] = entry.getValue();//频率

}

}

}

举例来说：对于 '一 一@中'，pair数组是如何保存这对词的词共现频率的呢？

'一 一'在 map 中第0号位置处，它是一元核心词典中的第34个词。 共有22个共现词。如下：

其中，第一个共现词是 '一 一 @中'，就是'一 一'与 '中' 共同出现，出现的频率为1。而 ''中'' 在一元核心词典中的 4124行，如下图所示：

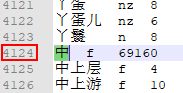
因此，'一 一@中'的pair数组存储如下：

0=4123 （‘中’在一元核心词典中的位置（从下标0开始计算））

1=1 （'一 一@中'的词共现频率）

2=5106 （'为' 在一元核心词典中的位置） 【为 p 65723】

3=6 ('一 一@为'的词共现频率)

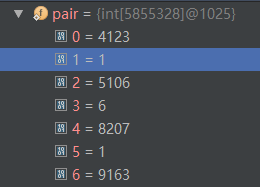
由此可知，对于二元核心词典共现词而言，共同前缀的后续词 在 pair数组中是顺序存储的，比如说：前缀'一 一'的所有后缀：中、为、交谈……按顺序依次在 pair 数组中存储。而这也是能够对 pair 数组进行二分查找的基础。

一 一@中 1

一 一@为 6

一 一@交谈 1

一 一@介绍 1

一 一@作 1

一 一@分析

.......//省略其他

二分查找

现在来看看 二分查找是干什么用的？为什么减少了二分查找的范围。为了获取某 两个词（idA 和 idB） 的词共现频率，需要进行二分查找：

public static int getBiFrequency(int idA, int idB){

//省略其他代码

int index = binarySearch(pair, start[idA], start[idA + 1] - start[idA], idB);

return pair[index + 1];

}

根据前面介绍，start[idA + 1] - start[idA]就是以 idA 为前缀的 所有词的 词共现频率。比如，以 '一 一' 为前缀的词一共有22个，假设我要查找 '一 一@向' 的词共现频率是多少？在核心二元词典文件CoreNatureDictionary.ngram.txt中，我们知道 '一 一@向' 的词共现频率为2，但是：如何用程序快速地实现查找呢？

二元核心词典的总个数还是很多的，比如在HanLP1.5.3大约有290万个二元核心词条，如果每查询一次 idA@idB 的词共现频率就要从290万个词条里面查询，显然效率很低。若先定位出 所有以 idA 为前缀的共现词：idA@xx1，idA@xx2，idA@xx3……，然后再从从这些 以idA为前缀的共现词中进行二分查找，来查找 idA@idB，这样查找的效率就快了许多。

而start 数组保存了一元词典中每个词 在二元词典中的词共现情况： start[idA] 代表 idA在 pair 数组中共现词的起始位置，而start[idA + 1] - start[idA]代表 以idA 为前缀的共现词一共有多少个，这样二分查找的范围就只在 start[idA] 和 start[idA] + (start[idA + 1] - start[idA]) - 1之间了。

private static int binarySearch(int[] a, int fromIndex, int length, int key)

{

int low = fromIndex;

int high = fromIndex + length - 1;

//省略其他代码

说到这里，再多说一点：二元核心词典的二分查找 是为了获取 idA@idB 的词共现频率，而这个词共现频率的用处之一就是最短路径分词算法(维特比分词)，用来计算最短路径的权重。关于最短路径分词，可参考这篇解析：

//只列出关键代码

List<Vertex> vertexList = viterbi(wordNetAll);//求解词网的最短路径

to.updateFrom(node);//更新权重

double weight = from.weight + MathTools.calculateWeight(from, this);//计算两个顶点(idA->idB)的权重

int nTwoWordsFreq = CoreBiGramTableDictionary.getBiFrequency(from.wordID, to.wordID);//查核心二元词典

int index = binarySearch(pair, start[idA], start[idA + 1] - start[idA], idB);//二分查找 idA@idB共现频率

总结

有时候由于特定项目需要，需要修改核心词典。比如添加一个新的二元词共现词条 到 二元核心词典中去，这时就需要注意：添加的新词条需要存在于一元核心词典中，否则添加无效。另外，添加到CoreNatureDictionary.ngram.txt里面的二元共现词的位置不太重要，因为相同的前缀 共现词 都会保存到 同一个TreeMap中，但是最好也是连续放在一起，这样二元核心词典就不会太混乱。

文章来源 hapjin的博客