Codeforces Round #369 (Div. 2) D. Directed Roads dfs求某个联通块的在环上的点的数量

D. Directed Roads

 

ZS the Coder and Chris the Baboon has explored Udayland for quite some time. They realize that it consists of n towns numbered from 1to n.

There are n directed roads in the Udayland. i-th of them goes from town i to some other town ai (ai ≠ i). ZS the Coder can flip the direction of any road in Udayland, i.e. if it goes from town A to town B before the flip, it will go from town B to town A after.

ZS the Coder considers the roads in the Udayland confusing, if there is a sequence of distinct towns A1, A2, ..., Ak (k > 1) such that for every 1 ≤ i < k there is a road from town Ai to town Ai + 1 and another road from town Ak to town A1. In other words, the roads are confusing if some of them form a directed cycle of some towns.

Now ZS the Coder wonders how many sets of roads (there are 2n variants) in initial configuration can he choose to flip such that after flipping each road in the set exactly once, the resulting network will not be confusing.

Note that it is allowed that after the flipping there are more than one directed road from some town and possibly some towns with no roads leading out of it, or multiple roads between any pair of cities.

Input

The first line of the input contains single integer n (2 ≤ n ≤ 2·105) — the number of towns in Udayland.

The next line contains n integers a1, a2, ..., an (1 ≤ ai ≤ n, ai ≠ i), ai denotes a road going from town i to town ai.

Output

Print a single integer — the number of ways to flip some set of the roads so that the resulting whole set of all roads is not confusing. Since this number may be too large, print the answer modulo 109 + 7.

Examples

input

3
2 3 1

output

6

 

Note

Consider the first sample case. There are 3 towns and 3 roads. The towns are numbered from 1 to 3 and the roads are , ,  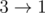initially. Number the roads 1 to 3 in this order.

The sets of roads that ZS the Coder can flip (to make them not confusing) are {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}. Note that the empty set is invalid because if no roads are flipped, then towns 1, 2, 3 is form a directed cycle, so it is confusing. Similarly, flipping all roads is confusing too. Thus, there are a total of 6 possible sets ZS the Coder can flip.

The sample image shows all possible ways of orienting the roads from the first sample such that the network is not confusing.

题意：

　　n个点得图

　　给你n条边，a[i] 表示 i指向a[i]

　　现在你可以改变某些边的方向是的 图中不存在环

　　问你有多少种方案

题解：

　　总共有2^n

　　对于这个图，我们视为无向。

　　我们要明白 是由多个联通块 组成的 联通块中有可能存在环

　　那么定义一个 联通快 上 在环上的 点数是 num , 这个联通块有all个点，之后我们给定方向，利用num,all我们就可以求出 这个联通块不存在环的 方案数了

　　那么 对于答案 就是所有联通快不存在环 的 方案数 的乘积

　

#include<bits/stdc++.h>
using namespace std;

#pragma comment(linker, "/STACK:102400000,102400000")
#define ls i<<1
#define rs ls | 1
#define mid ((ll+rr)>>1)
#define pii pair<int,int>
#define MP make_pair

typedef long long LL;
const long long INF = 1e18;
const double Pi = acos(-1.0);
const int N = 2e5+, M = 1e6+, inf = 2e9, mod = 1e9+;

int n,mx = -,f[N],al,num;
int deep[N],vis[N];
vector<int >G[N];
void add(int u,int v){
    G[u].push_back(v);
}

LL quick_pow(LL x,LL p) {
    if(!p) return ;
    LL ans = quick_pow(x,p>>);
    ans = ans*ans%mod;
    if(p & ) ans = ans*x%mod;
    return ans;
}

void dfs(int u,int fa,int dep) {
        al++;
        deep[u] = dep;
        vis[u] = ;
        for(int i = ; i < G[u].size(); ++i) {
            int to = G[u][i];
            if(!vis[to])dfs(to,u,dep+);else if(to!=fa) num = (abs(deep[to] - deep[u]) + );
        }
}
LL in[N];
int main() {
        LL ans = ;
        in[] = ;
        scanf("%d",&n);
        for(int i = ; i < N; ++i) in[i] = 1LL * in[i-] *  % mod;

        for(int i = ; i <= n; ++i) {scanf("%d",&f[i]);add(i,f[i]);add(f[i],i);}

        for(int i = ; i <= n; ++i) {
            al = num = ;
            if(vis[i]) continue;
            dfs(i,,);
            if(al == ) num = ;
            ans = (ans * (in[num]-2LL) % mod * in[al-num]) % mod;
        }
        printf("%I64d\n",(ans+mod) % mod);
        return ;
}