最长公共子序列(Longest common subsequence)

问题描述：

给定两个序列 X=<x1, x2, ..., xm>, Y<y1, y2, ..., yn>，求X和Y长度最长的公共子序列。(子序列中的字符不要求连续)

这道题可以用动态规划解决。定义c[i, j]表示Xi和Yj的LCS的长度，可得如下公式：

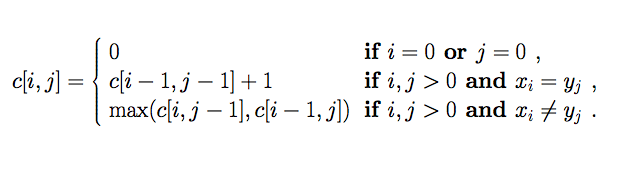
伪代码如下：

C++实现：

int longestCommonSubsequence(string x, string y)
{
    int m = x.length();
    int n = y.length();
    vector< vector<int> > c(m + , vector<int>(n + ));

    for (int i = 0; i <= m; ++i)
        c[i][] = ;
    for (int j = 1; j <= n; ++j)
        c[][j] = ;
    for (int i = ; i <= m; ++i)
    {
        for (int j = ; j <= n; ++j)
        {
            if (x[i-] == y[j-])
                c[i][j] = c[i-][j-] + ;
            else if (c[i-][j] >= c[i][j-])
                c[i][j] = c[i-][j];
            else
                c[i][j] = c[i][j-];
        }
    }
    return c[m][n];
}

后记：

我本来以为我已经掌握了LCS，其实不过是记住了LCS的状态转移方程。15号参加了创新工场2016校园招聘笔试，题目要求打印出LCS，我就懵逼了。其实《算法导论》里讲的清清楚楚啊。

贴一下我的C++实现：

vector< vector<int> > b;    //辅助数组
void LCS(string x, string y)
{
    int m = x.length();
    int n = y.length();

    vector< vector<int> > c(m + , vector<int>(n + ));
    for (int i = ; i <= m; ++i)
        c[i][] = ;
    for (int j = ; j <= n; ++j)
        c[][j] = ;

    b.resize(m+);
    for (int i = ; i <= m; i++)
    {
        b[i].resize(n+);
    }
    for (int i = ; i <= m; i++)
        for (int j = ; j <= n; j++)
        {
            b[i][j] = ;
        }

    for (int i = ; i <= m; ++i)
    {
        for (int j = ; j <= n; ++j)
        {
            if (x[i-] == y[j-])
            {
                c[i][j] = c[i-][j-] + ;
                b[i][j] = ;    //
            }
            else if (c[i-][j] >= c[i][j-])
            {
                c[i][j] = c[i-][j];
                b[i][j] = ;   //
            }
            else
            {
                c[i][j] = c[i][j-];
                b[i][j] = ;   //
            }
        }
    }

}

void printLCS(vector< vector<int> > &b, string x, int i, int j)
{
    if (i ==  || j == )
        return ;
    if (b[i][j] == )
    {
        printLCS(b, x, i-, j-);
        printf("%c", x[i-]);
    }
    else if (b[i][j] == )
        printLCS(b, x, i-, j);
    else
        printLCS(b, x, i, j-);

}

阿里、腾讯、创新工场全部笔试跪；网易互联网简历挂；明天去面百度和华为，加油！！！