DFS+BFS(广度优先搜索弥补深度优先搜索遍历漏洞求合格条件总数)--09--DFS+BFS--蓝桥杯剪邮票

题目描述

如下图, 有12张连在一起的12生肖的邮票。现在你要从中剪下5张来，要求必须是连着的。（仅仅连接一个角不算相连） 
 
比如，下面两张图中，粉红色所示部分就是合格的剪取。 
 
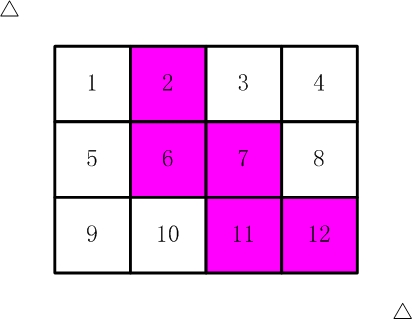
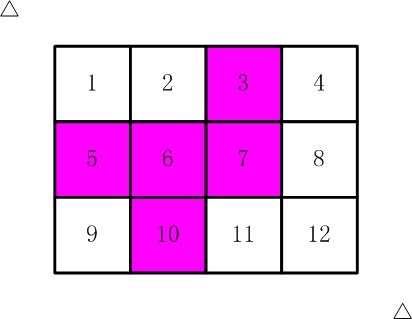
请你计算，一共有多少种不同的剪取方法。 

输出

请填写表示方案数目的整数。 

 

分析1

          使用开锁解锁机制、通过DFS一边搜索一边计数，每积累5个方格就停止进一步搜索，同时将结果存储起来。

　　　但是3、5、6、7、10（如图）此种情况是DFS做不到的，以下代码只用了DFS，只能得到82种结果。

 #include <iostream>
 #include <vector>
 #include <stdio.h>
 #include <queue>
 #include <cmath>
 #include <algorithm>
 using namespace std;
 const int ROW = ;
 const int COL = ;
 int sum = ;
 int num = ;
 int dd[][] = {{,},{,},{,-},{-,}};
 vector<vector<int> >a(ROW,vector<int>(COL,-));
 vector<int>sig[];
 vector<int>zz;
 vector<int>temp;
 void rightload(){
     sig[sum] = temp;
 }
 bool checkrightload(){
     temp = zz;
     sort(temp.begin(),temp.end());
     for(int i = ;i < sum;i++){
         if(sig[i] == temp)
             return false;
     }
     return true;
 }
 void lock(int i,int j){
     num++;
     a[i][j] = i*COL+j;
     zz.push_back(a[i][j]);
 }
 void unlock(int i,int j){
     num--;
     a[i][j] = -;
     zz.pop_back();
 }
 void dfs(int i,int j){
     for(int zz = ;zz < ;zz++){
         int ii = i + dd[zz][];
         int jj = j + dd[zz][];
         if(ii < ||jj < ||ii >= ROW||jj >= COL)
             continue;
         if(a[ii][jj] == -){
             lock(ii,jj);
             if(num == ){
                 if(checkrightload()){
                     rightload();
                     sum++;
                 }
             }
             else
                 dfs(ii,jj);
             unlock(ii,jj);
         }
     }
 }
 int main(){
     for(int i = ;i < ROW;i++){
         for(int j = ;j < COL;j++){
             lock(i,j);
             dfs(i,j);
             unlock(i,j);
         }
     }
     for(int i = ;i < sum;i++){
         for(int j =  ;j < ;j++){
             cout <<sig[i][j] <<" ";
         }
         cout <<endl;
     }
     cout << sum <<endl;
     return ;
 }

分析2

　　  为了弥补分析1所提出的漏洞，需要用BFS与DFS相结合，才能得到所有情况，以下是BFS与DFS结合解题的代码。

 #include <iostream>
 #include <vector>
 #include <stdio.h>
 #include <queue>
 #include <cmath>
 #include <algorithm>
 using namespace std;
 const int ROW = ;
 const int COL = ;
 int sum = ;
 int num = ;
 int dd[][] = {{,},{,},{,-},{-,}};
 vector<vector<int> >a(ROW,vector<int>(COL,-));
 vector<int>sig[];
 vector<int>zz;
 vector<int>temp;
 queue<pair<int,int> >myque;
 void rightload(){
     sig[sum] = temp;
 }
 bool checkrightload(){
     temp = zz;
     sort(temp.begin(),temp.end());
     for(int i = ;i < sum;i++){
         if(sig[i] == temp)
             return false;
     }
     return true;
 }
 void lock(int i,int j){
     num++;
     a[i][j] = i*COL+j;
     zz.push_back(a[i][j]);
 }
 void unlock(int i,int j){
     num--;
     a[i][j] = -;
     zz.pop_back();
 }
 void bfs(int i,int j){
     for(int zz = ;zz >= ;zz--){
         int ii = i + dd[zz][];
         int jj = j + dd[zz][];
         if(ii < ||jj < ||ii >= ROW||jj >= COL)
             continue;
         if(a[ii][jj] == -){
             myque.push({ii,jj});
         }
     }
     while(!myque.empty()){
         int ii = myque.front().first;
         int jj = myque.front().second;
         myque.pop();
         lock(ii,jj);
         if(num == ){
             if(checkrightload()){
                 rightload();
                 sum++;
             }
         }
         else{
             bfs(ii,jj);
         }
         unlock(ii,jj);
     }
 }
 void dfs(int i,int j){
     for(int zz = ;zz < ;zz++){
         int ii = i + dd[zz][];
         int jj = j + dd[zz][];
         if(ii < ||jj < ||ii >= ROW||jj >= COL)
             continue;
         if(a[ii][jj] == -){
             lock(ii,jj);
             if(num == ){
                 if(checkrightload()){
                     rightload();
                     sum++;
                 }
             }
             else{
                 dfs(ii,jj);
             }
             bfs(i,j);
             unlock(ii,jj);
         }
     }
 }
 int main(){
     for(int i = ;i < ROW;i++){
         for(int j = ;j < COL;j++){
             lock(i,j);
             dfs(i,j);
             unlock(i,j);
         }
     }
     for(int i = ;i < sum;i++){
         for(int j =  ;j < ;j++){
             cout <<sig[i][j] <<" ";
         }
         cout <<endl;
     }
     cout << sum <<endl;
     return ;
 }