FOC 转子初始位置检测（图文详解）

本文介绍了PMSM的转子初始位置的各种情况；

文章目录

1 什么是转子的初始位置？
2 如何让转子运行到初始位置？
3 iq=IDC;id=0;θ=0i_{q}=I_{DC} ;i_{d}=0;\theta = 0iq=IDC;id=0;θ=0

1 什么是转子的初始位置？

其实转子的初始位置是不确定的，但是在电机启动的时候，我们需要得到电角度，这样才可以进行矢量控制；所以，这里将转子与A轴重合作为初始位置，此时电角度也恰好为零，具体如下图所示；

)

至于原理下面会详细分析，这样在转子到初始位置后，也可以得到准确的电角度，就可以实现磁场和转子的同步转动。

2 如何让转子运行到初始位置？

其实这是一个很简单的问题，在这里我将它放大了，简单地分析了一下推导了一下，首先我们期望的结果是转子和A轴重合，准确地说是转子磁链和A轴重合。

之前在分析单电阻采样，对不同时刻的转子位置，处于不同的扇区时，电流的状态做了简单的分类讨论，首先看下图；

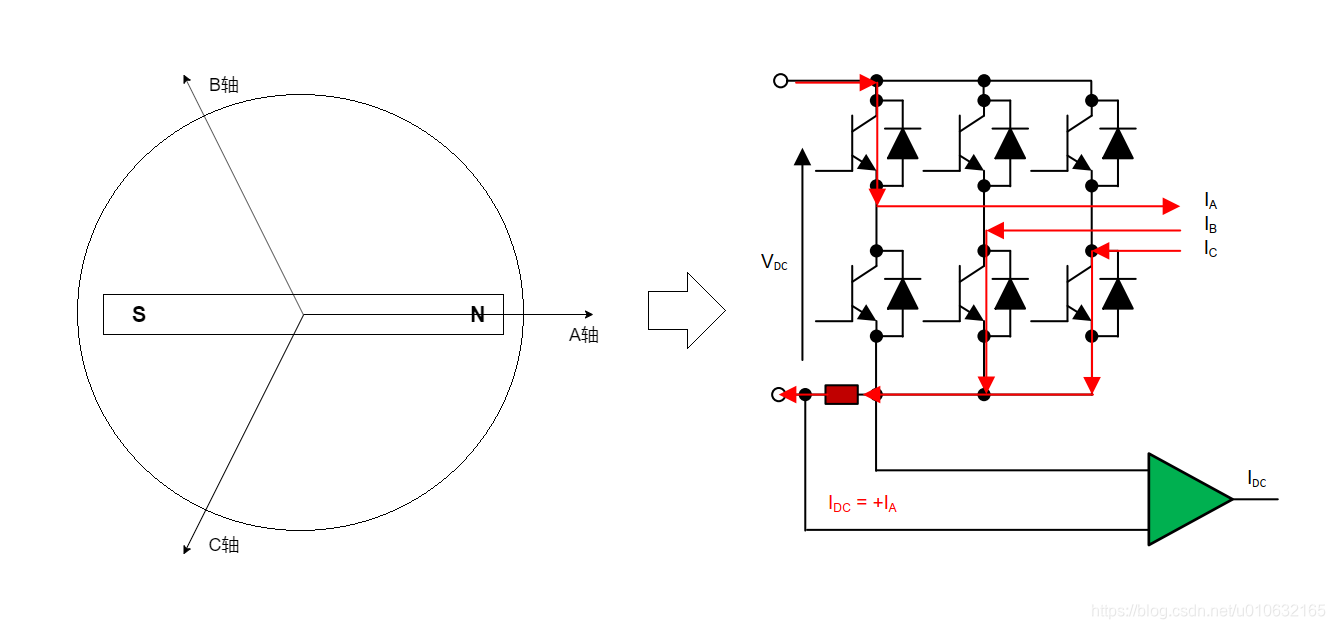
显然，当转子磁链与A轴重合的时候，逆变器的开关状态为：

SA:SB:SC—1:0:0
S_{A}:S_{B}:S_{C}—1:0:0
SA:SB:SC—1:0:0

这里规定上管打开，下管关闭的时候，SA=1S_{A} = 1SA=1；上管关闭，下管打开的时候，SA=0S_{A} = 0SA=0

因此可以得到

IA=IDCIC=IB=−IDC2I_{A} = I_{DC} \\
\\
\\
I_{C} = I_{B} = -\cfrac{ I_{DC}}{2} \\
IA=IDCIC=IB=−2IDC

静止坐标系αβ\alpha\betaαβ，α\alphaα轴的电流分量为iαi_{\alpha}iα，iβi_{\beta}iβ，则Clark变换满足以下公式：

iα=iAiβ=13∗iA+23∗iBi_{\alpha} = i_{A} \\
\\
i_{\beta} = \cfrac{1}{\sqrt{3}}*i_{A}+\cfrac{2}{\sqrt{3}}*i_{B}iα=iAiβ=31∗iA+32∗iB

所以根据Clark变换公式可以得到：

iα=IA=IDCiβ=13∗IA+23∗IB=13IDC−13IDC=0i_{\alpha} = I_{A} = I_{DC}\\
\\
i_{\beta} = \cfrac{1}{\sqrt{3}}*I_{A}+\cfrac{2}{\sqrt{3}}*I_{B} = \cfrac{1}{\sqrt{3}} I_{DC} - \cfrac{1}{\sqrt{3}} I_{DC} = 0iα=IA=IDCiβ=31∗IA+32∗IB=31IDC−31IDC=0

根据park变换：

id=iα∗cosθ+iβ∗sinθiq=−iα∗sinθ+iβ∗cosθi_{d}=i_{\alpha}*cos\theta+i_{\beta}*sin\theta \\
i_{q}=-i_{\alpha}*sin\theta+i_{\beta}*cos\thetaid=iα∗cosθ+iβ∗sinθiq=−iα∗sinθ+iβ∗cosθ

因为当前电角度为零，所以将 IA=IDC，IB=0，θ=0I_{A} = I_{DC}，I_{B} = 0 ，\theta = 0IA=IDC，IB=0，θ=0 代入park变换的公式中，最终得到；

id=IDCiq=0i_{d}=I_{DC} \\
i_{q}=0id=IDCiq=0

所以可以设置id=IDC,iq=0i_{d}=I_{DC} ,i_{q}=0id=IDC,iq=0；然后通过park反变换得到Uα,UβU_{\alpha},U_{\beta}Uα,Uβ输入到SVPWM，就可以将转子驱动的和A轴重合的位置。

		ipark_parameter.Ds = 0;

		ipark_parameter.Qs = 20000;

		ipark_parameter.Angle = 0;

		ipark_calc(&ipark_parameter);

		sv.Ualpha = ipark_parameter.Alpha;

		sv.Ubeta = ipark_parameter.Beta;

		svpwm_calc(&sv);

		svpwm_update(ipark_parameter.Qs, &sv);

以上代码是实际测试中使用的，20000是电流的Q格式，最终可以实现预期的效果。

那么，如果iq=IDC;id=0;θ=0i_{q}=I_{DC} ;i_{d}=0;\theta = 0iq=IDC;id=0;θ=0;转子会出现什么样的情况呢？

3 iq=IDC;id=0;θ=0i_{q}=I_{DC} ;i_{d}=0;\theta = 0iq=IDC;id=0;θ=0

因为存在机械角度和电角度存在：电角度=机械角度*极对数；

所以如果电机极对数为1时：转子磁链与A轴夹角的机械角度为90°

所以如果电机极对数为2时：转子磁链与A轴夹角的机械角度为45°