mode|平均数|方差|标准差|变异系数|四分位数|几何平均数|异众比率|偏态|峰态

应用统计学

数据的概括性度量

集中趋势

Mode众数是唯一描述无序类别数据，由图可知众数便是图形中的峰。

对于类别变量，众数就是某一种类别。

中位数和平均数都可能不是样本中的值。

中位数不受极值影响，对于类别数据来说，中位数是某一类别（同mode），各变量值与中位数的离差绝对值之和最小，与均数不同。

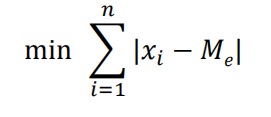
平均数的求法，令函数等于各变量值与平均数的离差平方之和，该函数表达如下式。

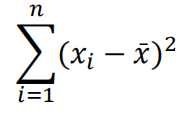
对该函数求一阶导，如下式，

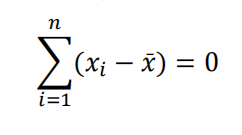
当一阶导为零时该函数取到最小值，此时样本均值表达式为：

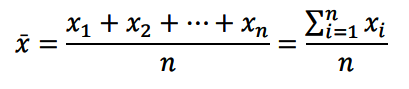
各变量值与平均数的离差平方之和最小，各变量值与中位数的离差绝对值之和最小。两性质验证如下表：

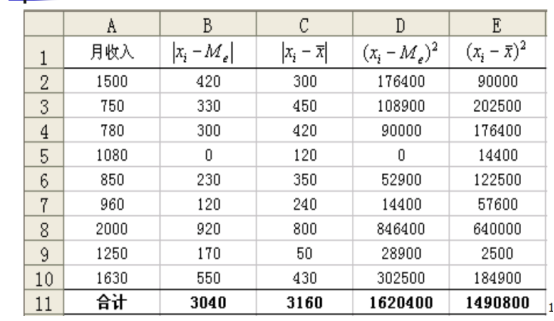
平均值可代数计算且无偏有效，所以数学属性比中位数好。

四分位数中上下四分位数有不同算法，算法的准确度也不同，但是n变大则各算法之间差距变小，同时变的更精确。

几何平均数推导：由以下公式转换，其中x值为比率。

100（1+G）=100（1+x1）（1+x2）（1+x3），等式变换之后得到G的表达式，该G值即为

应用：一种测量多次的平均数比一次测量更准确，样本均值的方差比随机变量的方差小，更准确。所以用样本均值的分布比总体分布的方差小。样本均值方差是总体分布方差/n.

离散趋势

因为平均值不能代表大多数情况，所以引入描述离散程度的特征值。

异众比率即与众数不一样观测值的比率，如下式。

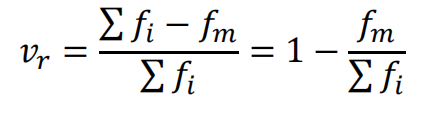
如果异众比率大，则其代表性不是很好。

四分位差：inter quartile range，即3/4处值-1/4处值。

极差：未考虑数据分布

平均差：离均差总和除以总数

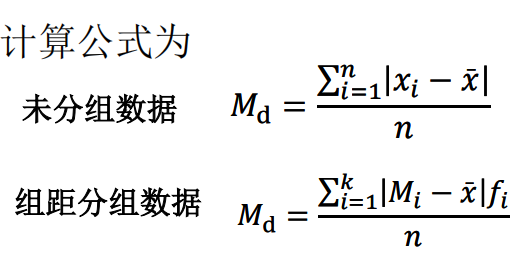
方差&标准差

为什么样本方差的分母为n-1？

若使用n作为分母，则用样本方差估计总体方差有偏。若使用样本方差则无偏。

2.自由度degree of freedom：指数据个数与附加给独立的观测值的约束或限制的个

数之差，即n-（约束个数）。所以就此例可知，要求样本方差，但其中除已知特征值外，还有一个样本均值的约束，所以样本方差的自由度为n-1。

除此之外还有变异系数，消除了数据水平高低和计量单位的影响。

偏态和峰态

偏态系数即表现数据分布的较正态分布的偏斜程度：

峰态系数即表现与标准正态分布比峰值的高低：