JS递归及二叉搜索树的移除节点

1递归含义：在某时某刻某个条件下调用包含自己的函数

2:注意点：⑴递归过程中一定要加限制条件，要不然会陷入死循环：

　　　　　　　　　　死循环eg：

function f(someP){
   f(somP);
}
f(4); //Uncaught RangeError: Maximum call stack size exceeded

　　　　　　　　　　正常调用：

//计算输入某个正整数，然后一直向下叠加 ，这里仅仅做一个简单示例，不进行输入num的判断
function f(num){
    let x;
    if(num>0){
        x =num + f(num-1);
        return x;
    }
    return false;
}

f(5);

⑵递归有个过程，不是一步到位的，这一点尤其重要，因为在学习JS数据结构与算法中的二叉搜索树的移除代码会至关重要，不懂递归过程的话很容易看不懂移除代码

function getSum(num){
     if(x === 1){
           return 1;
     }
     return num + getSum(num-1)
}

getSum(5);

　　　　　　过程如下：

　　　　　　　　　　①：getSum(5)调用函数并传入参数5，执行函数中的num +getSum(num-1) ->5+getSum(5-1)

　　　　　　　　　　②：getSum(4)调用函数并传入参数4，执行函数中的num+getSum(num-1) ->4+getSum(4-1)

　　　　　　　　　　③：getSum(3)调用函数并传入参数3，执行函数中的num+getSum(num-1) ->3+getSum(3-1)

　　　　　　　　　　④：getSum(2)调用函数并传入参数2，执行函数中的num+getSum(num-1) ->2+getSum(2-1)

　　　　　　　　　　⑤：getSum(1)调用函数并传入参数1，执行函数中的return 1；

　　　　　　　　　　⑥：这时候再一步一步往回走，即1+2+3+4+5；即可以理解为递归调用过程中，是不会立即计算的，要等到限制条件结束后，才会一步一步往上计算。

3：二叉搜索树的移除节点：移除节点程序是二叉搜索树程序方法中最复杂的一个。

　　　eg：

　　　　

class Node{    //节点类
  constructor(key){
    this.key = key;
    this.left = null;
    this.right = null;
  }
}
function defaultCompare(a, b) {  //比较函数
  if (a === b) {
    return Compare.EQUALS;
  }
  return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN;
}

const Compare = {
  LESS_THAN: -1,
  BIGGER_THAN: 1,
  EQUALS: 0
};
class BinarySearchTree{
  constructor(compareFn = defaultCompare){
    this.compareFn = compareFn;
    this.root = null;
  }
  remove(key){
    this.root = this.removeNode(this.root,key);
  }
  removeNode(node,key){
    if(node == null){
      return null;
    }
    if(this.compareFn(key,node.key) === Compare.LESS_THAN){      // (1)
      node.left = this.removeNode(node.left,key);                //(2)
      return  node;　　　　　　　　　　　　　　　　　　　　　　　　　　　　//(3)
    }else if (this.compareFn(key,node.key) === Compare.BIGGER_THAN){　　//(4)
      node.right = this.removeNode(node.right,key);　　　　　　　　　　　　//(5)
      return  node;　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　//(6)　
    }else{　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　//(7)
      if(node.left == null && node.right == null){  　　　　//(8)　　　　//第一种情况，移除一个叶节点（只有父节点没有子节点的节点）
        node = null;　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　//(9)
        return  node;　　　　　　　　　　　　　　　　　　　　　　　　　　　　　//(10)
      }
      if(node.left == null){　　　　　　　　　　　　　　　//第二种情况，移除有一个左or右子节点的节点
        node = node.right;　　　　　　　　　　　　　　　　　　　　　　　　　　//(11)
        return  node;　　　　　　　　　　　　　　　　　　　　　　　　　　　　　//(12)
      }else if(node.right == null) {
        node = node.left;                                            //(13)
        return node;　　　　　　　　　　　　　　　　　　　　　　　　　　　　　//(14)
      }
      const aux = this.minNode(node.right);         //(15) //第三种情况，移除有两个子节点的节点
      node.key = aux.key;　　　　　　　　　　　　　　　　//(16)
      node.right = this.removeNode(node.right,aux.key); //(17)
      return  node;　　　　　　　　　　　　　　　　　　　　　　//(18)
    }
  }
}
const tree1 = new BinarySearchTree();
tree1.remove(8);

　　　　假设现在有一个节点顺序为

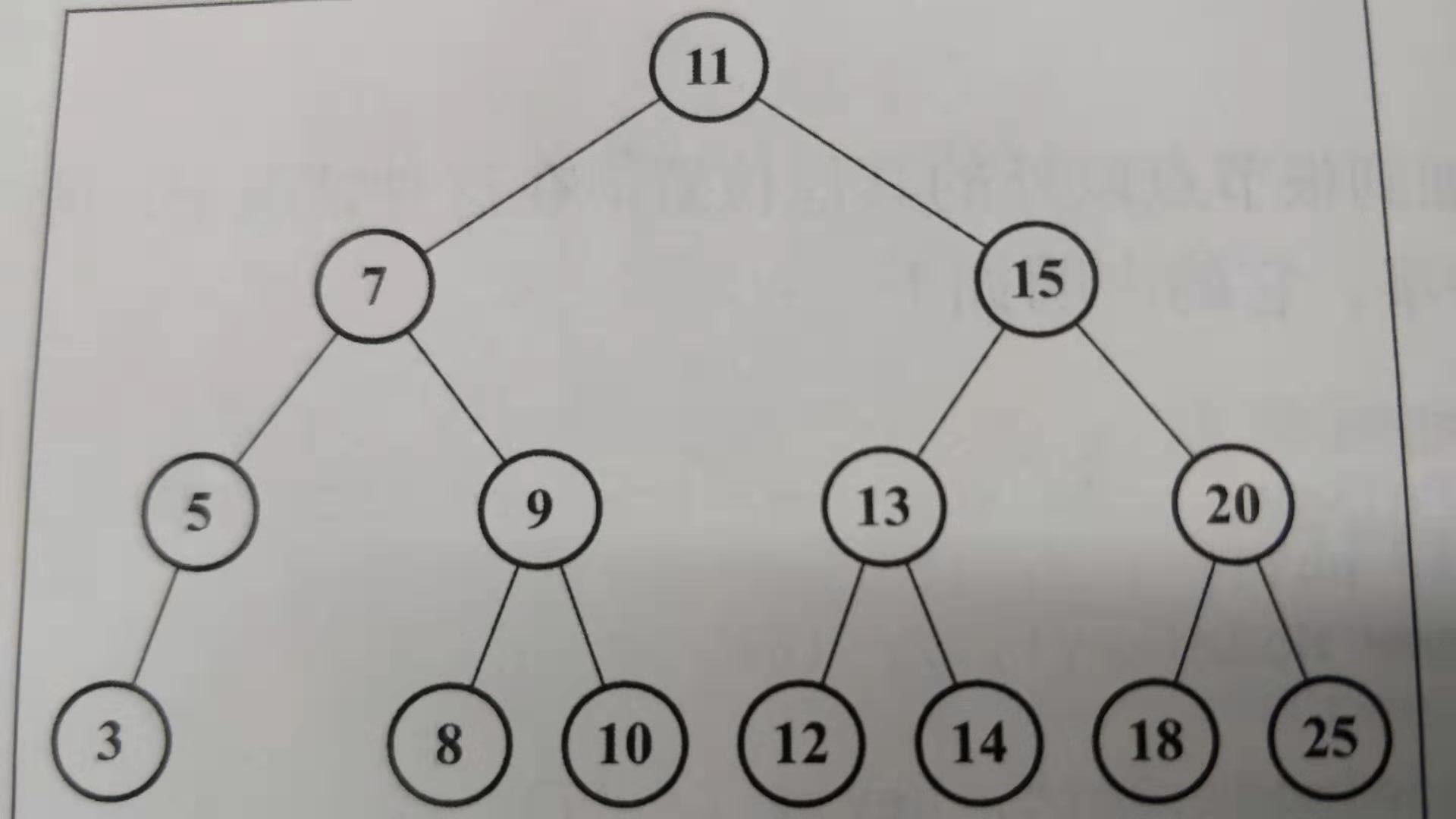
　　　　现在我们需要移除节点8，则代码的顺序应该是：

①：开始时key:8   node: Node{ key: 11, left : Node, right : Node}，进入行(1)，判断大小后进入行(2)，此时key:8   node: Node{ key: 7, left : Node, right : Node}

②：递归调用第一次，进入行(4)判断大小后进入行(5)，此时key:8   node: Node{ key: 9, left : Node, right : Node}

③：递归调用第二次，进入行(1)判断大小后进入行(2)，此时key:8   node: Node{ key: 8, left : null, right : null}

④：递归调用第三次，进入行(7 ，8， 9)，返回一个node，此时key: 8 ,node ：null；

⑤：进入行(3)，此时结果为： key:8 ,node:Node{key: 9 ,left:null,right:Node};

⑥：进入行(6)，此时结果为： key:8 ,node:Node{key: 9 ,left:Node,right:Node};

⑦：进入行(3)，此时结果为：key:8 ,node:Node{key: 11,left:Node,right:Node};

⑧：返回到remove()后，跳出程序，节点8已移除。

　　　备注1：上述步骤只实现了第一种情况，如果有需要，读者可以用chrome的调试工具进行断点调试，在Sources中可查看key及node的具体情况，

　　    备注2：这里很明显说明了递归调用的执行顺序，我就是因为不懂执行顺序，这段代码看了我2个多小时。。。。。切记切记，