机器学习降维--lu分解


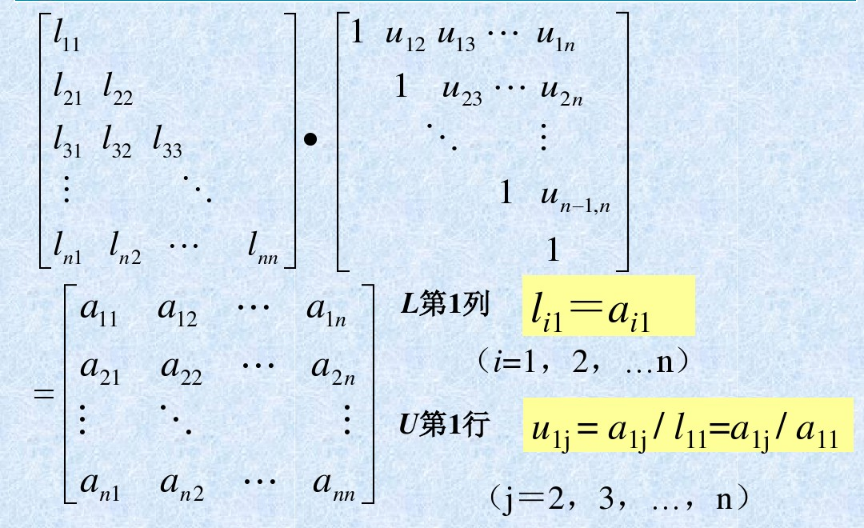
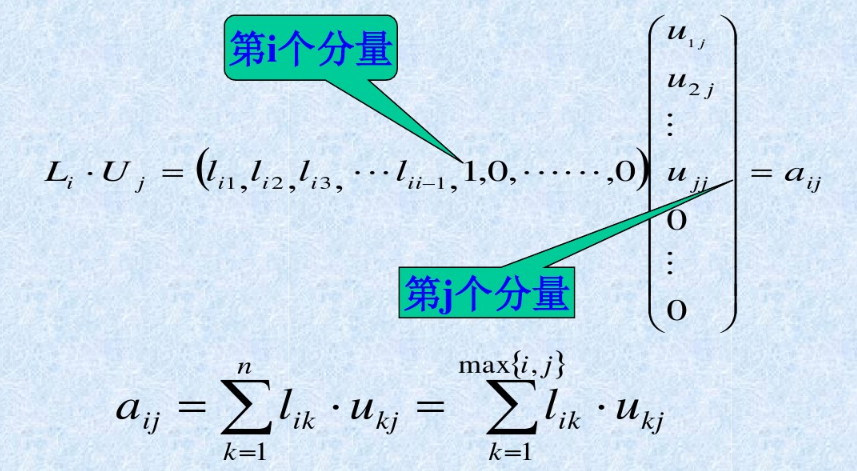




机器学习降维--lu分解的更多相关文章
- matlab 求解线性方程组之LU分解
线性代数中的一个核心思想就是矩阵分解,既将一个复杂的矩阵分解为更简单的矩阵的乘积.常见的有如下分解: LU分解:A=LU,A是m×n矩阵,L是m×m下三角矩阵,U是m×n阶梯形矩阵 QR分解: 秩分解 ...
- LU分解,Javascript代码
///A 为矩阵,这里写成一维数组,如 [1],[1,2,3,4] function GetLU(a) { var n = a.length;//矩阵的总数据数目 var s = Math.sqrt( ...
- 四大机器学习降维算法:PCA、LDA、LLE、Laplacian Eigenmaps
四大机器学习降维算法:PCA.LDA.LLE.Laplacian Eigenmaps 机器学习领域中所谓的降维就是指采用某种映射方法,将原高维空间中的数据点映射到低维度的空间中.降维的本质是学习一个映 ...
- matlab实现高斯消去法、LU分解
朴素高斯消去法: function x = GauElim(n, A, b) if nargin < 2 for i = 1 : 1 : n for j = 1 : 1 : n A(i, j) ...
- LU分解(2)
接着上次LU分解的讲解,这次给出使用不同的计算LU分解的方法,这种方法称为基于GaxPy的计算方法.这里需要了解lapapck中的一些函数.lapack中有一个函数名为gaxpy,所对应的矩阵计算公式 ...
- LU分解(1)
1/6 LU 分解 LU 分解可以写成A = LU,这里的L代表下三角矩阵,U代表上三角矩阵.对应的matlab代码如下: function[L, U] =zlu(A) % ZLU ...
- MATLAB矩阵的LU分解及在解线性方程组中的应用
作者:凯鲁嘎吉 - 博客园http://www.cnblogs.com/kailugaji/ 三.实验程序 五.解答(按如下顺序提交电子版) 1.(程序) (1)LU分解源程序: function [ ...
- 线性代数笔记10——矩阵的LU分解
在线性代数中, LU分解(LU Decomposition)是矩阵分解的一种,可以将一个矩阵分解为一个单位下三角矩阵和一个上三角矩阵的乘积(有时是它们和一个置换矩阵的乘积).LU分解主要应用在数值分析 ...
- 矩阵分解---QR正交分解,LU分解
相关概念: 正交矩阵:若一个方阵其行与列皆为正交的单位向量,则该矩阵为正交矩阵,且该矩阵的转置和其逆相等.两个向量正交的意思是两个向量的内积为 0 正定矩阵:如果对于所有的非零实系数向量x ,都有 x ...
随机推荐
- caffe-----使用C++ 提取网络中间层特征数据
最近实验,想要在c++下知道网络中间某一层的特征数据情况,查找了相关资料,记录一下. 其实在caffe框架里面是包含这种操作的,可以模仿tools/extract_features.cpp中的操作来得 ...
- 替换RTXLogo插件说明
一.包含Logo图标文件介绍 (一)桌面图标包含在RTX.exe (二)桌面右下角图标包含在MainFrameRes.dll (三)RTX设置图标包含在Config.dll (四)查看用户信息图标包含 ...
- 查询处理Oracle锁表的问题
--以下几个为相关表SELECT * FROM v$lock;SELECT * FROM v$sqlarea;SELECT * FROM v$session;SELECT * FROM v$proce ...
- cocos2dx基础篇(3) 常用重要类
---------------------------------------- 入口类main.cpp 主要控制类AppDelegate.cpp -------------------------- ...
- 小程序图片预览 wx.previewImage
list: [ 'http://img5.imgtn.bdimg.com/it/u=3300305952,1328708913&fm=26&gp=0.jpg', 'http://i ...
- poj1220(短除法实现任意进制转换)
题目链接:https://vjudge.net/problem/POJ-1220 题意:给定a进制的大数s,将其转换为b进制.其中2<=a,b<=62. 题意:一般进制转换是以10进制为中 ...
- IDEA Maven项目 pom.xml 找不到 Dependency 依赖
转载: IDEA Maven项目 pom.xml 找不到 Dependency 依赖 如果你的pom.xml中使用了dependencyManagement管理依赖并且添加了你本地仓库中不存在的依赖可 ...
- 组合&多态&封装
目录 组合&多态&封装 一.组合 1.1什么是组合 1.2 为什么要用组合 1.3 如何使用组合 1.4 继承和组合都在什么时候用 二.多态与多态性 2.1 什么是多态 2.2 如何用 ...
- python3小demo
总结常用的功能小实例,快速学习并掌握python技能 1.墨迹天气 import requests from lxml.html import etree import json import tim ...
- help_topic表,以字符拆分,一行转多行
help_topic表是数据库mysql下的一个表 SUBSTRING_INDEX(s, delimiter, number) 返回从字符串 s 的第 number 个 ...
