Ordering Cows

题意描述

好像找不到链接（找到了请联系作者谢谢），所以题目描述会十分详细：

Problem 1: Ordering Cows [Bruce Merry, South African Computer Olympiad, 2003]

Farmer John has noticed that when his N (1 <= N <= 1,500) cows line up to be milked, certain cows always line up ahead of certain other cows. He has made a list of L (1 <= L <= 10,000) pairs of cows for which he has noticed this. He wants to send this list to his friend, Farmer Bob. Unfortunately, the inter-farm cowmunication network is very slow.

FJ has realized that he can compress the list by removing redundant information. The information he has is all of the form "cow A lines up before cow B". Information is redundant if it can be deduced from

other information on the list. For example, given "Alice is before Betty", "Betty is before Carol" and "Alice is before Carol" the last statement is redundant. Of course, the cows are numbered with unique serial numbers in the range 1..N; only a few of them have names (and those are not used here).

Help Farmer John by finding the smallest subset of his list from which the rest of the list can be deduced. Happily, the answer is guaranteed to be unique, and the original list contains no contradictions such as "Alice before Betty" and "Betty before Alice".

PROBLEM NAME: order

INPUT FORMAT:

• Line 1: Two space-separated integers: N and L.

• Lines 2..L+1: Two integers X and Y (1 <= X,Y <= N), indicating that cow X lines up before cow Y. No fact is duplicated.

SAMPLE INPUT (file order.in):

5 6

3 5

4 2

5 2

2 1

3 1

4 1

OUTPUT FORMAT:

• Line 1: A single line with the number of facts that Farmer John will send to Farmer Bob.

• Lines 2..U+1: The facts from the input file that Farmer John will transmit. These must be lists in the same format as the entries in the input file. They must be sorted numerically on the first entry in the line, with ties being broken by the second entry on the line.

SAMPLE OUTPUT (file order.out):

4

2 1

3 5

4 2

5 2

OUTPUT DETAILS:

The facts "cow 3 before cow 1" and "cow 4 before cow 1" can be deduced from the 4 facts listed in the output. However, none of the output facts can be deduced from the others.

给你关于 \(N\) 个数的 \(L\) 对大小关系，其中关系 x y 表示 x>y。

如果有关系 x y 与关系 y z 那么显然关系 x z 是不必要的。

求出这 \(L\) 对关系中的最少必要关系。（即通过省下的这些关系可以推出被删去的关系）

写出其数量并按照以数字一为主关键字，以数字二为次关键字的顺序从小到大输出。

算法分析

类似传递闭包，但是这里要求你排除冗余的关系。

那么显然，如果我们可以确定一个顺序，保证后面的关系不会影响前面的关系。

那么只需要从前往后扫一遍，遇到多余的关系排除即可。（因为只有前面的关系可能影响后面的关系）

排除的方法之后再说。

确定方法的关系：

1. 将每个关系当做有向边建图，易证这是个 DAG 图。
2. 将此图拓扑排序，按照拓扑排序的顺序给各个节点从小到大赋值。
3. 按照每个关系的数字一拓扑值从大到小为主关键字，数字二拓扑值从小到大为次关键字排序。
4. 所得即上面所说的遍历顺序。

解释一下，我们给每个节点赋予一个 ”贡献值“，表示其对其它节点的影响力。

那么显然影响大的边要先考虑（这也符合上面的顺序）。

易得，拓扑值大的节点影响力也大，所以以其从大到小为主关键字。

但是，当从同一个点出发考虑关系时，就应当优先考虑拓扑值小的，理由如下：

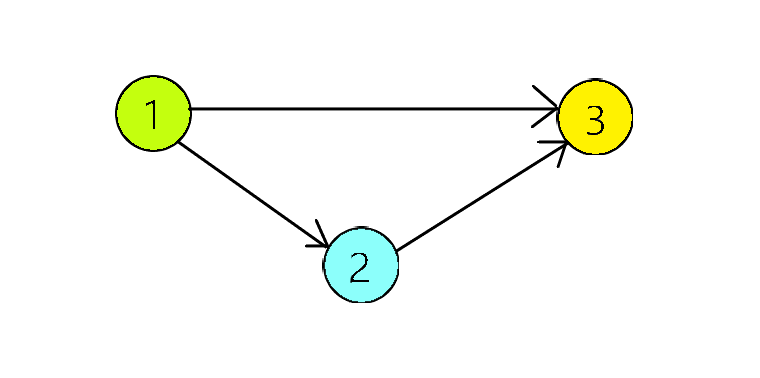
那么显然只有按照以从小到大为次关键字，才能将关系 1 3 排除。

然后就按照这个顺序往后排查即可，具体方法为状压 DP。

但是由于节点数量很多，所以要用到 C++ STL 的 bitset。

假设有关系 \(x\to y\)，如果 \(bits(x,y)\) 这个关系为多余关系。

否则 \(bits(x)|=bits(y)\)。

代码实现

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<cmath>
#include<bitset>
#include<queue>
#define N 1510
#define M 10010
using namespace std;

int n,m,head[N],cnt=0;
int ru[N],Topo[N],tot=0;
struct Edge{
	int nxt,to,frm;
}ed[M];
struct Ans{
	int u,v;
}ans[M];
bitset<N>bits[N];
queue<int>q;

int read(){
	int x=0,f=1;char c=getchar();
	while(c<'0' || c>'9') f=(c=='-')?-1:1,c=getchar();
	while(c>='0' && c<='9') x=x*10+c-48,c=getchar();
	return x*f;
}

void add(int u,int v){
	ed[++cnt].nxt=head[u];
	ed[cnt].frm=u;
	ed[cnt].to=v;
	head[u]=cnt;
	return;
}

void topo(){
	for(int i=1;i<=n;i++)
		if(!ru[i]) q.push(i);
	while(!q.empty()){
		int u=q.front();q.pop();
		Topo[u]=++tot;
		for(int i=head[u];i;i=ed[i].nxt)
			if(!--ru[ed[i].to]) q.push(ed[i].to);
	}
	return;
}

bool cmp(Edge a,Edge b){
	if(a.frm!=b.frm)
		return Topo[a.frm]>Topo[b.frm];
	return Topo[a.to]<Topo[b.to];
}

bool cnp(Ans a,Ans b){
	if(a.u!=b.u) return a.u<b.u;
	return a.v<b.v;
}

int main(){
	//freopen("order.in","r",stdin);
	//freopen("order.out","w",stdout);
	memset(ru,0,sizeof(ru));
	n=read(),m=read();
	for(int i=1;i<=m;i++){
		int u=read(),v=read();
		add(u,v);++ru[v];
	}
	topo();//简简单单的拓扑排序。
	sort(ed+1,ed+m+1,cmp);
	for(int i=1;i<=n;i++)
		bits[i][i]=true;//预处理。
	tot=0;
	for(int i=1;i<=m;i++){
		int u=ed[i].frm,v=ed[i].to;
		if(bits[u][v]) continue;
		bits[u]=bits[u]|bits[v];//DP。
		ans[++tot]=(Ans){u,v};
	}
	sort(ans+1,ans+tot+1,cnp);
	printf("%d\n",tot);
	for(int i=1;i<=tot;i++)
		printf("%d %d\n",ans[i].u,ans[i].v);
	//fclose(stdin);fclose(stdout);
	return 0;
}

完结撒花。