贝塞尔曲线（B-spline）的原理与应用

什么是贝塞尔曲线？

贝塞尔曲线(Bézier curve)，又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。

来源

贝塞尔曲线于1962，由法国工程师皮埃尔·贝塞尔（Pierre Bézier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau演算法开发，以稳定数值的方法求出贝兹曲线。

贝塞尔曲线完全由其控制点决定其形状,　ｎ个控制点对应着ｎ－１阶的贝塞尔曲线，并且可以通过递归的方式来绘制.

特点

贝塞尔曲线形状完全由控制点控制，有n个控制点就对应n-1阶的贝塞尔曲线。

Tip：下面公式中，B指曲线中点的集合，P指点，t指变化时间

线性公式：

给定点P0、P1，线性贝兹曲线只是一条两点之间的直线。这条线由下式给出：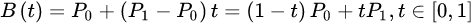

且其等同于线性插值。

二次方公式

二次方贝兹曲线的路径由给定点P0、P1、P2的函数B（t）追踪：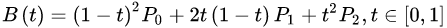

TrueType字型就运用了以贝兹样条组成的二次贝兹曲线。

三次方公式

P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝兹曲线。曲线起始于P0走向P1，并从P2的方向来到P3。一般不会经过P1或P2；这两个点只是在那里提供方向资讯。P0和P1之间的间距，决定了曲线在转而趋进P3之前，走向P2方向的“长度有多长”。
曲线的参数形式为：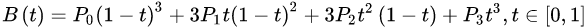

现代的成象系统，如PostScript、Asymptote和Metafont，运用了以贝兹样条组成的三次贝兹曲线，用来描绘曲线轮廓。

一般参数公式

阶贝兹曲线可如下推断。给定点P0、P1、…、Pn，其贝兹曲线即：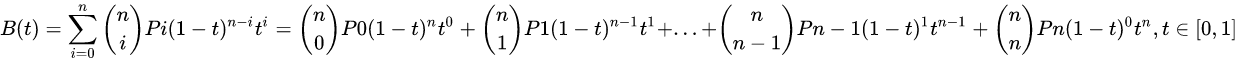

如上公式可如下递归表达： 用表示由点P0、P1、…、Pn所决定的贝兹曲线。
用平常话来说，阶的贝兹曲线，即双阶贝兹曲线之间的插值。