因子分解机 FM

特征组合

人工方式的特征工程，通常有两个问题：

特征爆炸
大量重要的特征组合都隐藏在数据中，无法被专家识别和设计

针对上述两个问题，广度模型和深度模型提供了不同的解决思路。

广度模型包括FM/FFM等大规模低秩(Low-Rank)模型，FM/FFM通过对特征的低秩展开，为每个特征构建隐式向量，并通过隐式向量的点乘结果来建模两个特征的组合关系实现对二阶特征组合的自动学习。作为另外一种模型，Poly-2模型则直接对2阶特征组合建模来学习它们的权重。FM/FFM相比于Poly-2模型，优势为以下两点。第一，FM/FFM模型所需要的参数个数远少于Poly-2模型：FM/FFM模型为每个特征构建一个隐式向量，所需要的参数个数为 \(O(km)\)，其中k为隐式向量维度，m为特征个数；Poly-2模型为每个2阶特征组合设定一个参数来表示这个2阶特征组合的权重，所需要的参数个数为 \(O(m^2)\)。第二，相比于Poly-2模型，FM/FFM模型能更有效地学习参数：当一个2阶特征组合没有出现在训练集时，Poly-2模型则无法学习该特征组合的权重；但是FM/FFM却依然可以学习，因为该特征组合的权重是由这2个特征的隐式向量点乘得到的，而这2个特征的隐式向量可以由别的特征组合学习得到。总体来说，FM/FFM是一种非常有效地对二阶特征组合进行自动学习的模型。
深度学习是通过神经网络结构和非线性激活函数，自动学习特征之间复杂的组合关系。目前在APP推荐领域中比较流行的深度模型有FNN/PNN/Wide & Deep。FNN模型是用FM模型来对Embedding层进行初始化的全连接神经网络。PNN模型则是在Embedding层和全连接层之间引入了内积/外积层，来学习特征之间的交互关系。Wide & Deep模型由谷歌提出，将LR和DNN联合训练，在Google Play取得了线上效果的提升。

FM 因子分解

FM算法可以在线性时间内完成模型训练, 是一个非常高效的模型。FM最大特点和优势：FM模型对稀疏数据有更好的学习能力，通过交互项可以学习特征之间的关联关系，并且保证了学习效率和预估能力。
One-Hot编码的特点: 大部分样本的特征比较稀疏; 特征空间大。
通过观察大量的样本数据可以发现，某些特征经过关联之后，与label之间的相关性就会提高。如：“USA”与“Thanksgiving”、“China”与“Chinese New Year”这样的关联特征，对用户的点击有着正向的影响。
多项式模型是包含特征组合的最直观的模型。考虑到计算效率, 我们只讨论二阶多项式模型。

\[
y(x)=w_0+\sum_{i=1}^nw_ix_i+\sum_{i=1}^n\sum_{j=i+1}^nw_{ij}x_ix_j
\]
从这个公式可以看出，组合特征的参数一共有\(n(n−1)\over 2\)个，任意两个参数都是独立的。当组合特征的样本数不充足时, 学习到的参数将不准确, 从而会严重影响模型预测的效果（performance）和稳定性。
那么，如何解决二次项参数的训练问题呢？矩阵分解提供了一种解决思路。在Model-based的协同过滤中，一个rating矩阵可以分解为user矩阵和item矩阵，每个user和item都可以采用一个隐向量表示。矩阵W就可以分解为 \(W=V^TV\)，V 的第j列便是第 j 维特征的隐向量。每个参数 \(w_{ij}=⟨v_i,v_j⟩\)，这就是FM模型的核心思想。因此，FM的模型方程为

\[
y(x)=w_0+\sum _{i=1}^nw_ix_i+\sum_{i=1}^n\sum_{j=i+1}^n⟨vi,vj⟩x_ix_j \\
⟨v_i,v_j⟩=\sum_{f=1}^kv_{i,f}·v_{j,f}
\]

隐向量的长度为k(k<<n)，包含k个描述特征的因子。
上边这个公式是一个通用的拟合方程，可以采用不同的损失函数用于解决回归、二元分类等问题，比如可以采用MSE（Mean Square Error）损失函数来求解回归问题，也可以采用Hinge、Cross-Entropy损失来求解分类问题。当然，在进行二元分类时，FM的输出需要经过Sigmoid变换，这与Logistic回归是一样的。

当前的FM公式的复杂度是\(\mathcal O(kn^2)\)，但是，通过下面的等价转换，可以将FM的二次项化简，其复杂度可以优化到\(\mathcal O(kn)\)，即：

\[
\sum_{i=1}^n\sum_{j=i+1}^n⟨v_i,v_j⟩x_i,x_j=\frac{1}{2}\sum_{f=1}^k[(\sum_{i=1}^nv_{i,f}x_i)^2-\sum_{i=1}^nv_{i,f}^2x_i^2]
\]
详细推导：

\[
\begin{align}
&\sum_{i=1}^n\sum_{j=i+1}^n⟨v_i,v_j⟩x_ix_j \\
=&\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n⟨v_i,v_j⟩x_ix_j-\frac{1}{2}\sum_{i=1}^n⟨v_i,v_i⟩x_ix_i \\
=&\frac{1}{2}(\sum_{i=1}^n\sum_{j=1}^n\sum_{f=1}^kv_{i,f}v_{j,f}x_ix_j-\sum_{i=1}^n\sum_{f=1}^kv_{i,f}v_{i,f}x_ix_i) \\
=&\frac{1}{2}\sum_{f=1}^k[(\sum_{i=1}^nv_{i,f}x_i)·(\sum_{j=1}^nv_{j,f}x_j)-\sum_{i=1}^nv_{i,f}^2x_i^2] \\
=&\frac{1}{2}\sum_{f=1}^k[(\sum_{i=1}^nv_{i,f}x_i)^2- \sum_{i=1}^nv_{i,f}^2x_i^2]
\end{align}
\]

FM模型的核心作用可以概括为以下三个：

FM降低了交叉项参数学习不充分的影响：one-hot编码后的样本数据非常稀疏，组合特征更是如此。为了解决交叉项参数学习不充分、导致模型有偏或不稳定的问题。作者借鉴矩阵分解的思路：每一维特征用k维的隐向量表示，交叉项的参数\(w_{ij}\)用对应特征隐向量的内积表示，即\(⟨v_i,v_j⟩\)。这样参数学习由之前学习交叉项参数\(w_{ij}\)的过程，转变为学习n个单特征对应k维隐向量的过程。
FM提升了模型预估能力。可以用于预估训练集中没有出现过的特征组合项.
FM提升了参数学习效率：是在多项式模型基础上对参数的计算做了调整，成为线性复杂度. 从交互项的角度看，FM仅仅是一个可以表示特征之间交互关系的函数表法式，可以推广到更高阶形式，即将多个互异特征分量之间的关联信息考虑进来。例如在广告业务场景中，如果考虑User-Ad-Context三个维度特征之间的关系，在FM模型中对应的degree为3。

与其他模型相比，它的优势如下：

FM是一种比较灵活的模型，通过合适的特征变换方式，FM可以模拟二阶多项式核的SVM模型、MF模型、SVD++模型等；
相比SVM的二阶多项式核而言，FM在样本稀疏的情况下是有优势的；而且，FM的训练/预测复杂度是线性的，而二项多项式核SVM需要计算核矩阵，核矩阵复杂度就是N平方。

FFM（场感知分解机,Field-aware Factorization Machine）

FM的缺点: 由于需要两两组合特征, 这样任意两个交叉特征之间都有了直接或者间接的关联, 因此任意两组特征交叉组合的隐向量都是相关的, 这实际上限制了模型的复杂度. 但是如果使得任意一对特征组合都是完全独立的, 这与通过核函数计算特征交叉类似, 有着极高的复杂性和自由度, 模型计算十分复杂. FFM正好介于这两者之间.
FFM引入特征组(field)的概念来优化此问题. FFM把相同性质的特征归于同一个field, 按照级别分别计算当前特征与其它field的特征组合时的特征向量, 这样特征组合的数量将大大减少.
假设样本的 n 个特征属于 f 个field，那么FFM的二次项有 nf个隐向量。而在FM模型中，每一维特征的隐向量只有一个。FM可以看作FFM的特例，是把所有特征都归属到一个field时的FFM模型。FFM模型方程如下:

\[
y(x)=w_0+\sum_{i=1}^nw_ix_i+\sum_{i=1}^n\sum_{j=i+1}^n⟨v_{i,fj},v_{j,f_i}⟩x_ix_j \\
\]

如果隐向量长度为k, 那么FFM的二次项参数就有nfk个,远多余FM的nk个.
由于FFM的任意两组交叉特征的隐向量都是独立的, 可以取得更好的组合效果, 这也使得FFM二次项并不能够化简，其复杂度为\(\mathcal O(kn^2)\)。

权重求解:
libFFM的实现中采用的是AdaGrad随机梯度下降方法. 并且在FFM公式中省略了常数项和一次项，模型方程如下:

\[
ϕ(w,x)=\sum_{j1,j2∈C_2}⟨w_{j_1,f_2},w_{j_2,f_1}⟩x_{j_1}x_{j_2}
\]
其中，C2是非零特征的二元组合，j1是特征，属于field f1，\(w_{j_1,f_2}\)是特征 j1对field f2 的隐向量。此FFM模型采用logistic loss作为损失函数，和L2惩罚项，因此只能用于二元分类问题。

\[
\underset{w}{\min}\sum_{i=1}^n\log(1+\exp{−y_iϕ(w,x_i)})+\frac{λ}{2}‖w‖^2
\]

DeepFM

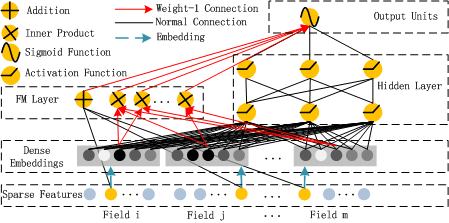
DeepFM模型结合了广度和深度模型的优点，联合训练FM模型和DNN模型，来同时学习低阶特征组合和高阶特征组合。此外，DeepFM模型的Deep部分和FM部分共享Embedding层输入，这样Embedding层的隐式向量在(残差反向传播)训练时可以同时接受到两部分的信息，从而使Embedding层的信息表达更加准确。DeepFM相对于现有的广度模型、深度模型以及Wide & Deep模型的优势在于：

DeepFM模型同时对低阶特征组合和高阶特征组合建模，从而能够学习到各阶特征之间的组合关系；
DeepFM模型是一个端到端的模型，不需要额外的人工特征工程。

FM/FFM与其它模型对比

vs 神经网络. 神经网络难以直接处理高维稀疏的离散特征, 因为这导致神经元的连接参数太多. 而因子分解机可以看作对高维稀疏的离散特征做嵌入(Embedding).
vs 梯度提升树. 当数据不是高度稀疏时,梯度提升树可以有效地学习到比较复杂的特征组合; 但是在高度稀疏的数据中, 特征二阶组合的数量超过样本的模式数量, 因而梯度梯度提升树无法学习到这种高阶组合.

参考

DeepFM paper: https://arxiv.org/abs/1703.04247
http://www.sohu.com/a/195238714_354898