Problem 6 二分

$des$
有 $n$ 个物品，第 $i$ 个物品有两个属性 $k_i, b_i$ ，表示它在时刻 $x$ 的价值为 $k_i

\times x + b_i$ .
当前处于时刻 $0$ ，你可以选择不超过 $m$ 个物品，使得存在某个整数时刻 $t$, $t >= 0$

，你选择的所有物品的总价值大于等于 $S$ .
给出 $S$，求 $t$ 的最小值。

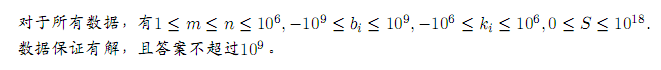
$sol$
选择任意一个集合，得到的收益和都可以表示为一个一次函数的形式。只关心这些
一次函数的最大值，可以发现这个最大值一定是先降后增的（当 t 非常大时，$k_i \times t > b_i$, 也有可能是单调递增或者单调递减）。
因此只需要 check 一下 0 时刻是否符合条件，如果不符合则进行二分。
注意 check 的时候只需要找出最大的 m 个即可，因此可以 O(n) 地做，具体做法是快排
的过程中只递归一边。直接用 STL 的 nth_element() 即可。
时间复杂度 $O(nlog10^9)$

$code$

#include <bits/stdc++.h>

#define Rep(i, j, k) for (int i = j; i <= k; i++)

using namespace std;

int Read() {
    char c = getchar(); int x = ;
    int sig = ;
    while (c < '' || c > '') { if (c == '-') sig = -; c = getchar(); }
    while (c >= '' && c <= '') x = x *  + c - '', c = getchar();
    return x * sig;
}

const int N = 1e6 + ;

typedef long long LL;

int n, m;
LL S;

int k[N], b[N];
LL val[N];

bool check(int x) {
    Rep(i, , n) val[i] = 1ll * k[i] * x + b[i];
    nth_element(val + , val + m, val + n + , greater<LL>());
    LL sum = ;
    Rep(i, , m) if (val[i] >  && (sum += val[i]) >= S) return true;
    return false;
}

int main() {

    n = Read(), m = Read(); scanf("%lld", &S);
    Rep(i, , n) k[i] = Read(), b[i] = Read();

    if (check()) {puts(""); return ;}

    int L = , R = 1e9, Ans;
    while (L <= R) {
        int mid = (L + R) / ;
        if (check(mid)) Ans = mid, R = mid;
        else L = mid + ;
    }
    printf("%d\n", Ans);

    return ;
}