钉子和小球_DP

Description

有一个三角形木板,竖直立放，上面钉着n(n+1)/2颗钉子，还有(n+1)个格子（当n=5时如图1）。每颗钉子和周围的钉子的距离都等于d，每个格子的宽度也都等于d，且除了最左端和最右端的格子外每个格子都正对着最下面一排钉子的间隙。 
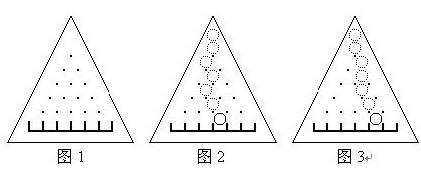
让一个直径略小于d的小球中心正对着最上面的钉子在板上自由滚落，小球每碰到一个钉子都可能落向左边或右边（概率各1/2），且球的中心还会正对着下一颗将要碰上的钉子。例如图2就是小球一条可能的路径。 
我们知道小球落在第i个格子中的概率pi=pi=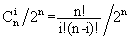，其中i为格子的编号，从左至右依次为0,1,...,n。 
现在的问题是计算拔掉某些钉子后，小球落在编号为m的格子中的概率pm。假定最下面一排钉子不会被拔掉。例如图3是某些钉子被拔掉后小球一条可能的路径。 

Input

第1行为整数n（2 <= n <= 50）和m（0 <= m <= n）。以下n行依次为木板上从上至下n行钉子的信息，每行中'*'表示钉子还在，'.'表示钉子被拔去，注意在这n行中空格符可能出现在任何位置。

Output

仅一行，是一个既约分数(0写成0/1)，为小球落在编号为m的格子中的概pm。既约分数的定义：A/B是既约分数，当且仅当A、B为正整数且A和B没有大于1的公因子。

Sample Input

5 2
*
   * .
  * * *
 * . * *
* * * * *

Sample Output

7/16

Source

【题意】在一块木板上，钉上钉子，排布成等边三角形。一个球从顶部开始，自由下落。每碰到一个钉子以后，等概率地向两边继续滚。现从该等边三角形的钉子中，拔去其中某些钉子。求这个球从顶部开始下落，滚到底部某个格子的概率。

思路：DP。逐步递推，分别计算每一层，滚到每一个口的概率。最后一层每个口的概率，就是对应底部每个格子的概率。每一个口的概率，若遇到一个钉子，则除以2后就是下一层对应两个口的概率；若没遇到钉子，则直接等于再下层的对应入口，即直接落下。一开始的初值，就是2^层数（2^50数值比较大用longlong型），即全部都是钉子时，第一个格子对应的概率。

#include<iostream>
#include<string.h>
#include<stdio.h>
using namespace std;
char s[];
char mp[][];
long long dp[][];
long long gcd(long long a,long long b)//求最大公约数
{
    if(!b) return a;
    else return gcd(b,a%b);
}
int main()
{
    int n,m;
    while(~scanf("%d%d",&n,&m))
    {
        for(int i=;i<=n;i++)
        {
            for(int j=;j<=i;j++)//空格可以无限多，字符串输入
            {
                cin>>s;
                mp[i][j]=s[];
            }
        }
        memset(dp,,sizeof(dp));
        dp[][]=1ll<<n;//dp是longlong型的，而1是int型的，所以在1后面加上ll，学了一招
        for(int i=;i<=n;i++)
        {
            for(int j=;j<=i;j++)
            {
                if(mp[i][j]=='*')//是钉子，往下滚的时候两个口子的概率都是一半；
                {
                    dp[i+][j]+=dp[i][j]>>;
                    dp[i+][j+]+=dp[i][j]>>;
                }
                else if(mp[i][j]=='.')//没有钉子，直接往下掉，但因为i行的第j个空对下来是第i+2行的j+1个空，这里要注意一点，刚开始理所当然的以为是j对j了....
                    dp[i+][j+]+=dp[i][j];
            }
        }
        long long w=dp[n+][m+];
        long long sum=;
        for(int i=;i<=n+;i++)
        {
            sum+=dp[n+][i];
        }
        long long k;
        k=gcd(sum,w);
        printf("%lld/%lld\n",w/k,sum/k);
    }
    return ;
}