TEST ON 平安夜

1.前言

　　= =

　　感觉自己其实没发过关于考试的博客过...

　　今天是一个平安的夜晚，漆黑的夜被霓虹划分成网络，很适合发题。

2.num9九数码问题

　　传统8数码改一下...只询问一个状态，所以很容易搞，正向广搜即可。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>

using namespace std;

const int maxn=+;

int ans[];
int level[];
int a[maxn][];
int que[maxn],rec[maxn],pre[maxn];
int Hash[maxn];

int get_h(int a[]){
    int sum=,cnt;
    for(int i=;i<;i++){
        cnt=;
        for(int j=i+;j<;j++)
            if(a[j]<a[i]) cnt++;
        sum+=cnt*level[-i];
    }
    return sum;
}

void change1(int L[],int N[]){
    N[]=L[],N[]=L[],N[]=L[];
    N[]=L[],N[]=L[],N[]=L[];
    N[]=L[],N[]=L[],N[]=L[];
}

void change2(int L[],int N[]){
    N[]=L[],N[]=L[],N[]=L[];
    N[]=L[],N[]=L[],N[]=L[];
    N[]=L[],N[]=L[],N[]=L[];
}

void print(int a[]){
    printf("%d %d %d\n%d %d %d\n%d %d %d\n\n",a[],a[],a[],a[],a[],a[],a[],a[],a[]);
}

void dfs(int p){
    if(!p) return;
    dfs(pre[p]);
    print(a[p]);
}

void BFS(){
    int H=,T=,key;

    pre[]=;key=get_h(a[]);Hash[key]=;que[]=key;

    while(H+<T){
        H++;
        change1(a[H],a[T]);
        key=get_h(a[T]);
        if(!Hash[key]){
            Hash[key]=Hash[que[H]]+,que[T]=key,rec[key]=T,pre[T]=H,T++;
            if(!key){
                int p=T-;
                printf("%d\n",Hash[]-);
                dfs(p);
                return ;
            }
        }

        change2(a[H],a[T]);
        key=get_h(a[T]);
        if(!Hash[key]){
            Hash[key]=Hash[que[H]]+,que[T]=key,rec[key]=T,pre[T]=H,T++;
            if(!key){
                int p=T-;
                printf("%d\n",Hash[]-);
                dfs(p);
                return ;
            }
        }
    }
    printf("UNSOLVABLE");
}

int main(){
    freopen("num9.in","r",stdin);
    freopen("num9.out","w",stdout);

    level[]=;
    for(int i=;i<=;i++) level[i]=level[i-]*i;

    for(int i=;i<;i++)
        scanf("%d",&a[][i]);

    BFS();
    return ;
}

3.lunch午餐问题

　　这种题看上去是贪心的样子，于是考场上先推一推式子，找找关系。

　　

　　感觉这一步还是比较好弄的，但是因为有两个队列，究竟放那一个去呢？

　　当时想，要不贪心放在等候时间较短的那边?

　　后来觉得不靠谱，因为要是下一个等待时间太长，导致后面的全部放了都没他慢，这时候放在更长的那边可能好些。

　　就想要不然增加几个选择，枚举一下每一列放几个？...可是枚举的时候出现问题了——没有考虑时间的影响，而是将时间作为结果放在的数组里。

　　事实上，只有两个都确定时，这个状态才算完全固定，而若是像我将前i个放j个在第一个队列这种其实不具有转移的性质的。

　　因为如果在f[i][j]取到最优值的时候，不一定时间上就是最优。所以说这样的转移不一定就是最优值，因为转移的时候调用了一个由转移得到的值！

　　事后终于醒悟了。感觉自己定这个状态就是为了转移方程好转移啊！

　　设计的时候一定要注意需要什么信息，什么信息可以用来转移，什么信息只是做一个结果。[果然这个叫信息竞赛啊...]感觉今天终于醒悟还是蛮好的。

　　上最后AC代码。

　　

#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int maxn=;
const int INF=0x7fffffff;

int n;
int ans;

struct Node{
    int a,b;
}s[maxn];

bool cmp(const Node &A,const Node &B){
    return A.b>B.b;
}

int sum[maxn];
int f[maxn][maxn*maxn];

int main(){
    freopen("lunch.in","r",stdin);
    freopen("lunch.out","w",stdout);

    scanf("%d",&n);
    for(int i=;i<=n;i++)
        scanf("%d%d",&s[i].a,&s[i].b);
    sort(s+,s+n+,cmp);
    for(int i=;i<=n;i++)
        sum[i]=sum[i-]+s[i].a;

    memset(f,0x7f,sizeof(f));
    f[][]=;
    for(int i=;i<=n;i++)
        for(int j=;j<=sum[i-];j++){
            f[i][j]=min(f[i][j],max(f[i-][j],sum[i-]-j+s[i].a+s[i].b));
            f[i][j+s[i].a]=min(f[i][j+s[i].a],max(f[i-][j],j+s[i].a+s[i].b));
        }

    ans=INF;
    for(int i=;i<=sum[n];i++)
        ans=min(ans,f[n][i]);

    printf("%d",ans);
    return ;
}

4.沼泽鳄鱼

5.梦幻折纸

　　

Problem

　　给一个N*M的格子，每个格子都写有一个1~N*M的数字。判断是否能将这张格子折叠成1*1，使得第1层标号为1，使得第2层标号为2...,第i层标号为i...。
　　1 7
　　3 1 7 6 5 4 2
　　AllRight

　　2 2
　　1 2
　　3 4
　　Cheat

　　2 3
　　2 1 6
　　3 4 5
　　Allright

　　4 4
　　11 12 15 14
　　10  9 16 13
　　 5  8  1  2
　　 6  7  4  3
　　Allright

　　对于四个样例，怎么才能折出来呢？

　　

　　好了...上面究竟怎么折只是娱乐而已。

　　分析本质啊，分析本质啊，剥茧抽丝寻找规律啊！

　　其实规律很简单...发现在最初网格中相邻的...它们最后一定因为纸的限制在一起咯 [所以单身狗才做不出...]

　　但是不同的情侣狗之间却有不同的人生方向

　　例如：

　　11 12 15 14
　　10  9 16 13
　　 5  8  1  2
　　 6  7  4  3

　　11-12是横向发展的，但是因为要折成一列，所以12-15和它虽然也是横向发展，却要和11-12不同的方向去折。

　　11-10是纵向发展的，同理，也有10-5和它方向不同。

　　所以总共有四个方向。

　　

　　我们再分析一下，对于一个中间的节点，就需要折向四个不同的方向。【泄水置平地，各自东西南北流】

　　但是两个相同方向的折纸，就不能有相交的元素，例如

　　1  3

　　2  4

　　1-3，2-4是方向完全相同的，但是因为两个相同的折纸一定不能相交。

　　

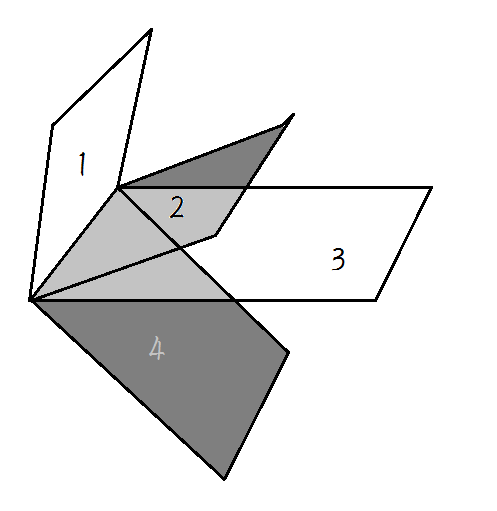
　　所以这种状态需要被排除，而如果没有这种状态，是不是就一定可行呢？

　　是的，因为除了这种情况外，其他的比如不同向的显然可以，同向包含的也不会出现穿越纸张这种事情了。

　　可是有人还是纠结于这个写在纸上，由一个矩形来翻折总觉得不顺手。

　　那现在就将你的大脑勾回变成一张矩形白纸，将每一列开始折叠，方向相同的之间不是包含就是相离，感觉还是很好的吧...

　　但是列上的，很多可能需要像样例4一样出现塞入这种操作。需要和行操作同时进行，有点难以想象，但是感觉只要符合了条件，进行折叠总是对的。

　　感受完毕，代码呈上。

#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int maxn=;

typedef int array[maxn][maxn];
array map, pam;

int t,n,m;
int link[maxn*maxn];

void newarc(int x,int y){
    if(x<y)
        link[x]=y,link[y]=-;
    else
        link[y]=x,link[x]=-;
}

bool check(int n,int m,array &map,int x){
    int i,j,top,stack[maxn*maxn];
    memset(link,,sizeof(link));

    for(int i=;i<n;i++)
        if((i&) == x)
            for(int j=;j<=m;j++)
                newarc(map[i][j],map[i+][j]);

    top=;
    for(int i=;i<=t;i++){
        if(link[i]>)
            stack[++top]=link[i];
        else if(link[i]<){
            if(stack[top]!=i) return false;
            top--;
        };
    }
    return true;
}

int main(){
    freopen("foldgirl.in","r",stdin);
    freopen("foldgirl.out","w",stdout);

    int kase;

    scanf("%d",&kase);
    while(kase--){
        scanf("%d%d",&n,&m);
        t=n*m;
        for(int i=;i<=n;i++)
            for(int j=;j<=m;j++)
                scanf("%d",&map[i][j]),pam[j][i]=map[i][j];

        if(check(n,m,map,) && check(n,m,map,) && check(m,n,pam,) && check(m,n,pam,))
            puts("AllRight");
        else
            puts("Cheat");
    }

    return ;
}