Jenkins系列之Jenkins的安装(一)
自动化测试的时候通常我们都会进行持续集成,下面是持续集成工具Jenkins的安装
Jenkins优点:
- 开源免费
- 跨平台,支持所有的平台
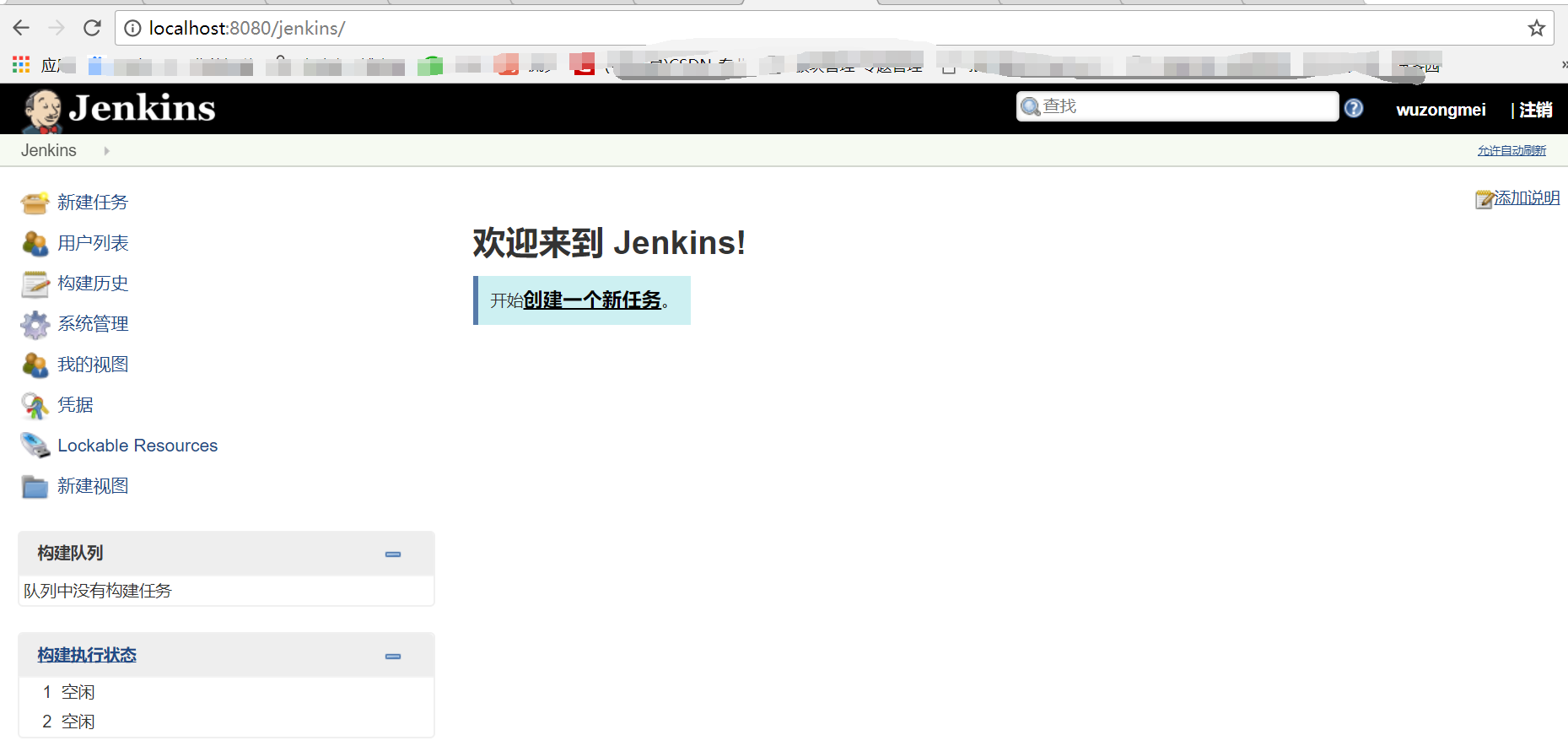
- web形式的可视化的管理页面
- 安装配置超级简单
- tips及时快速的帮助
- 有丰富的插件
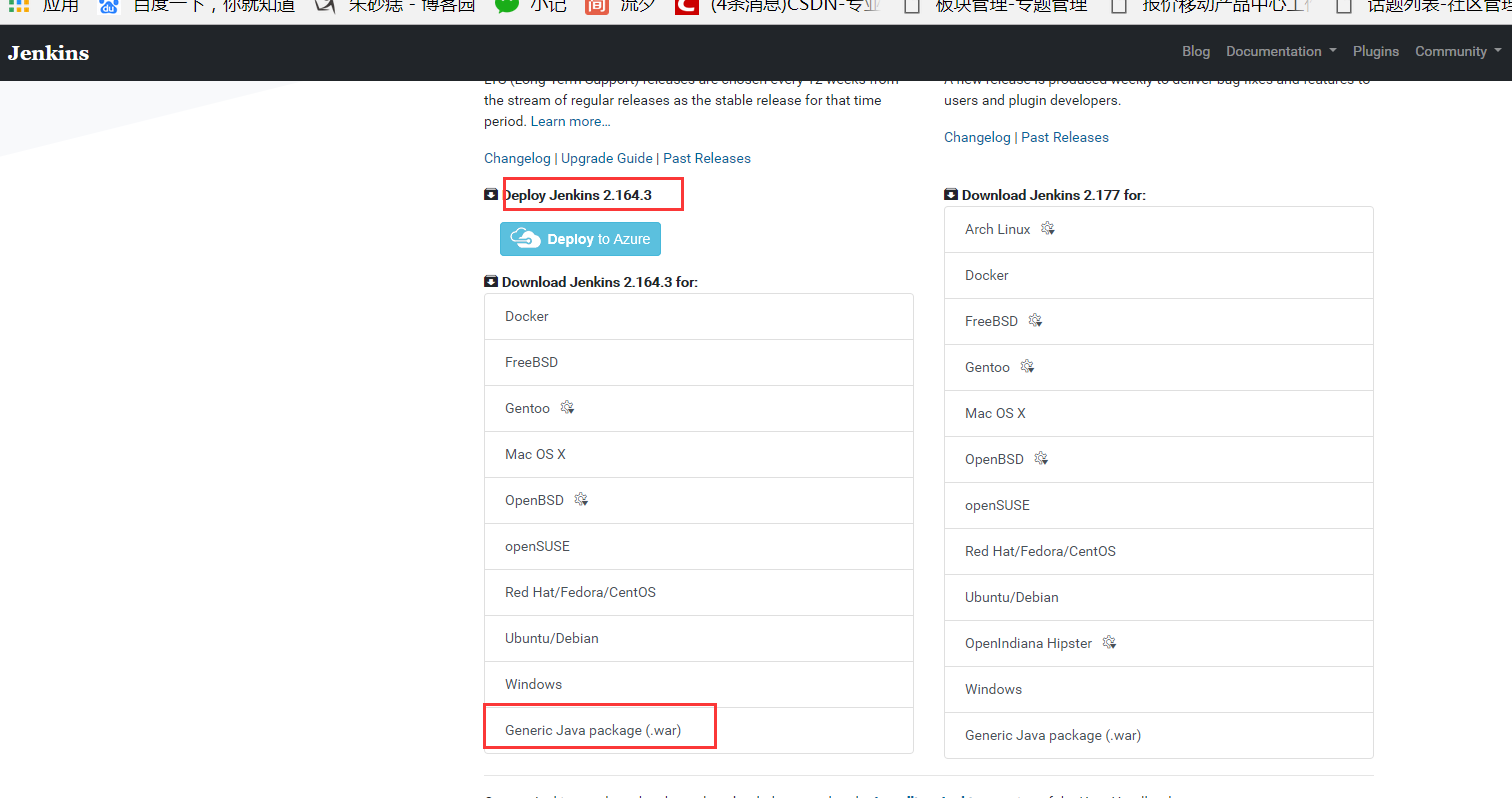
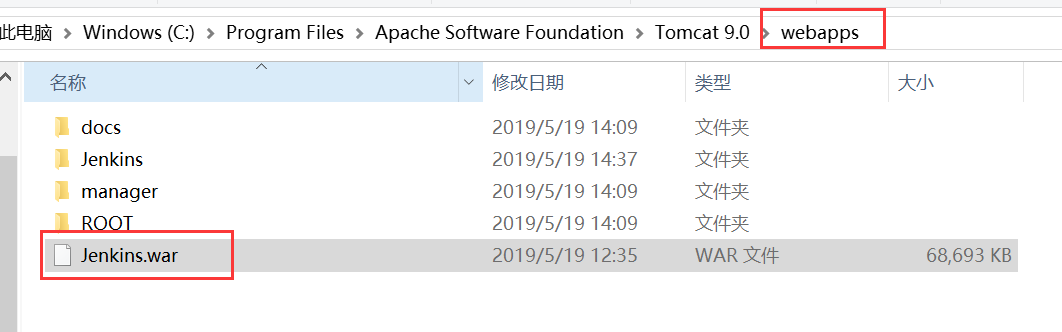
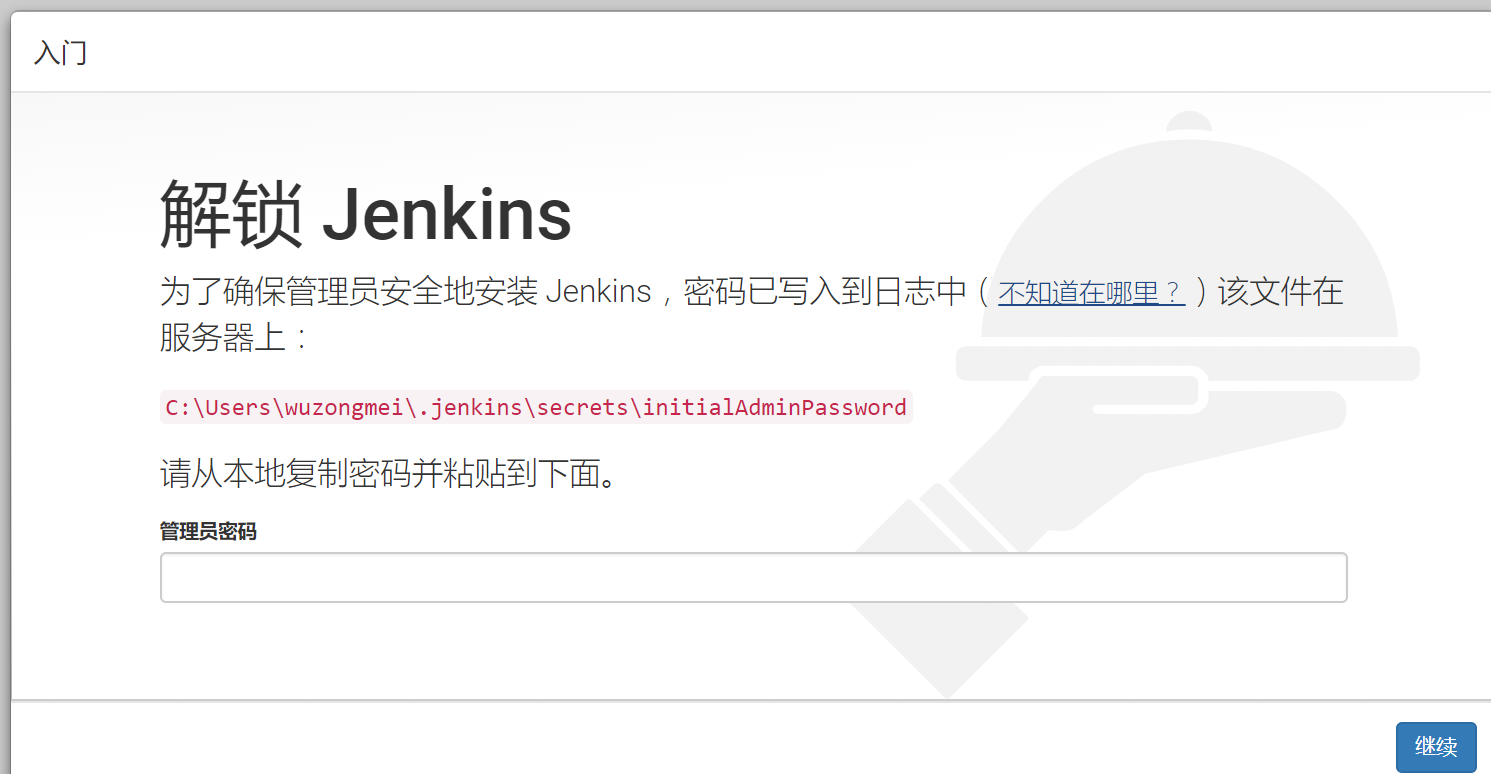
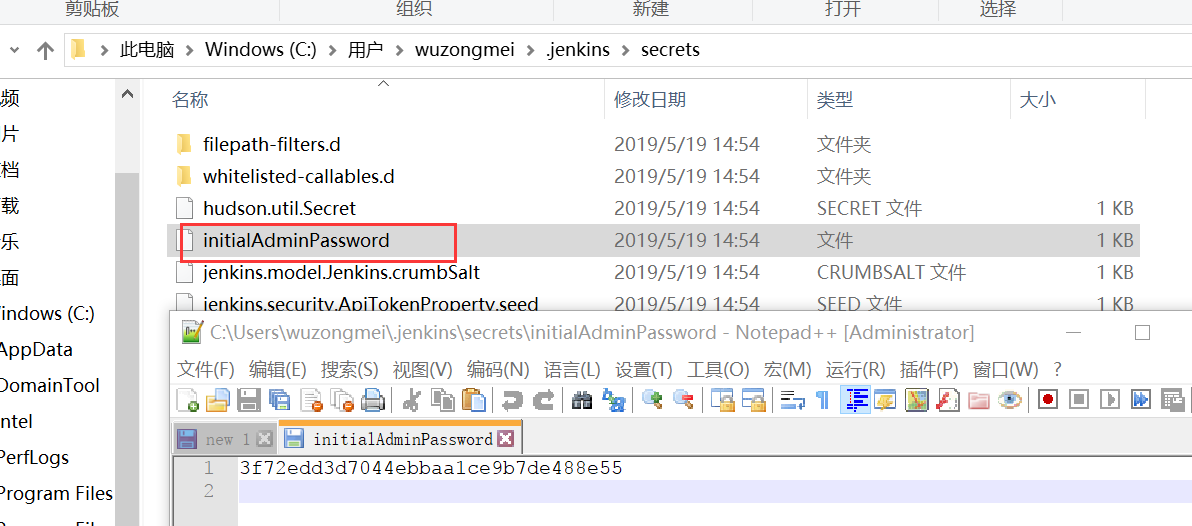
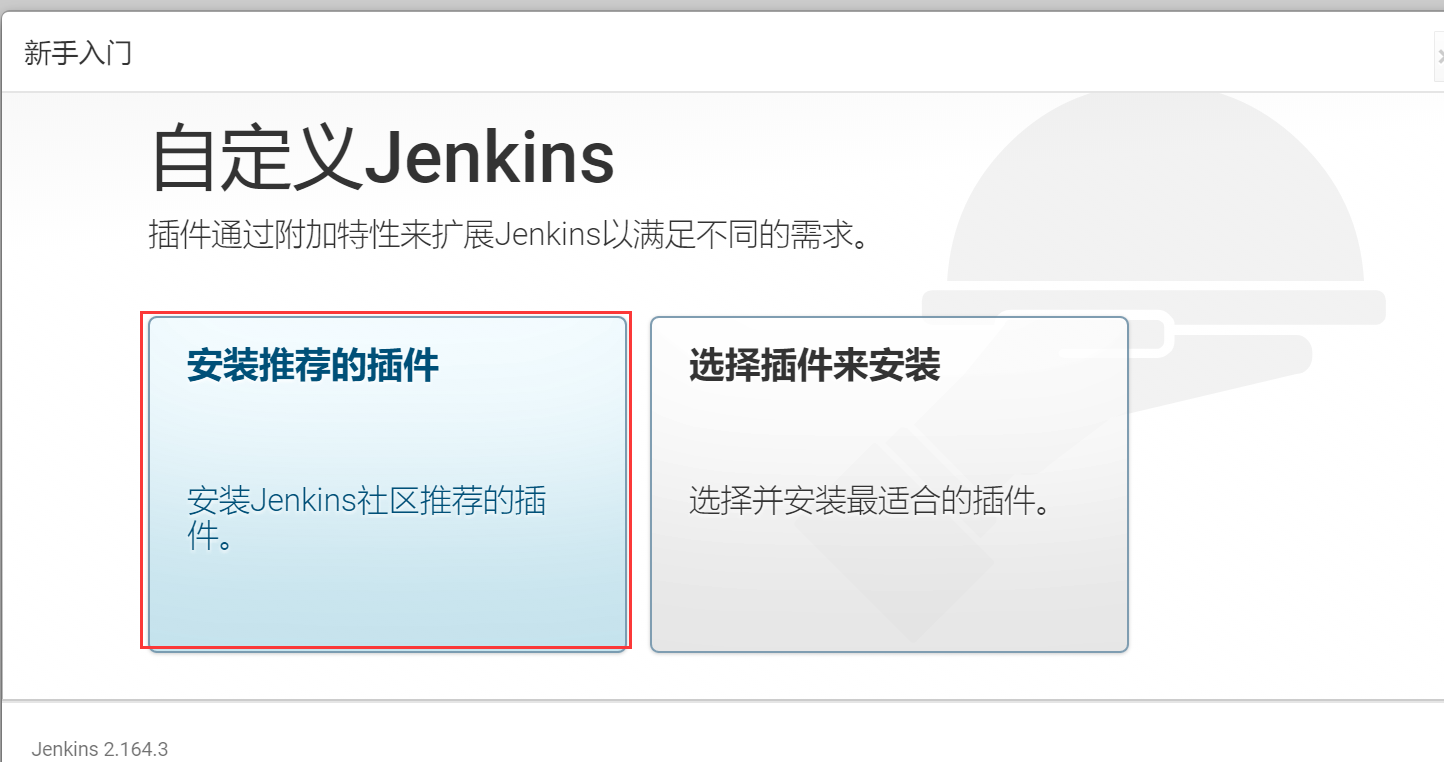
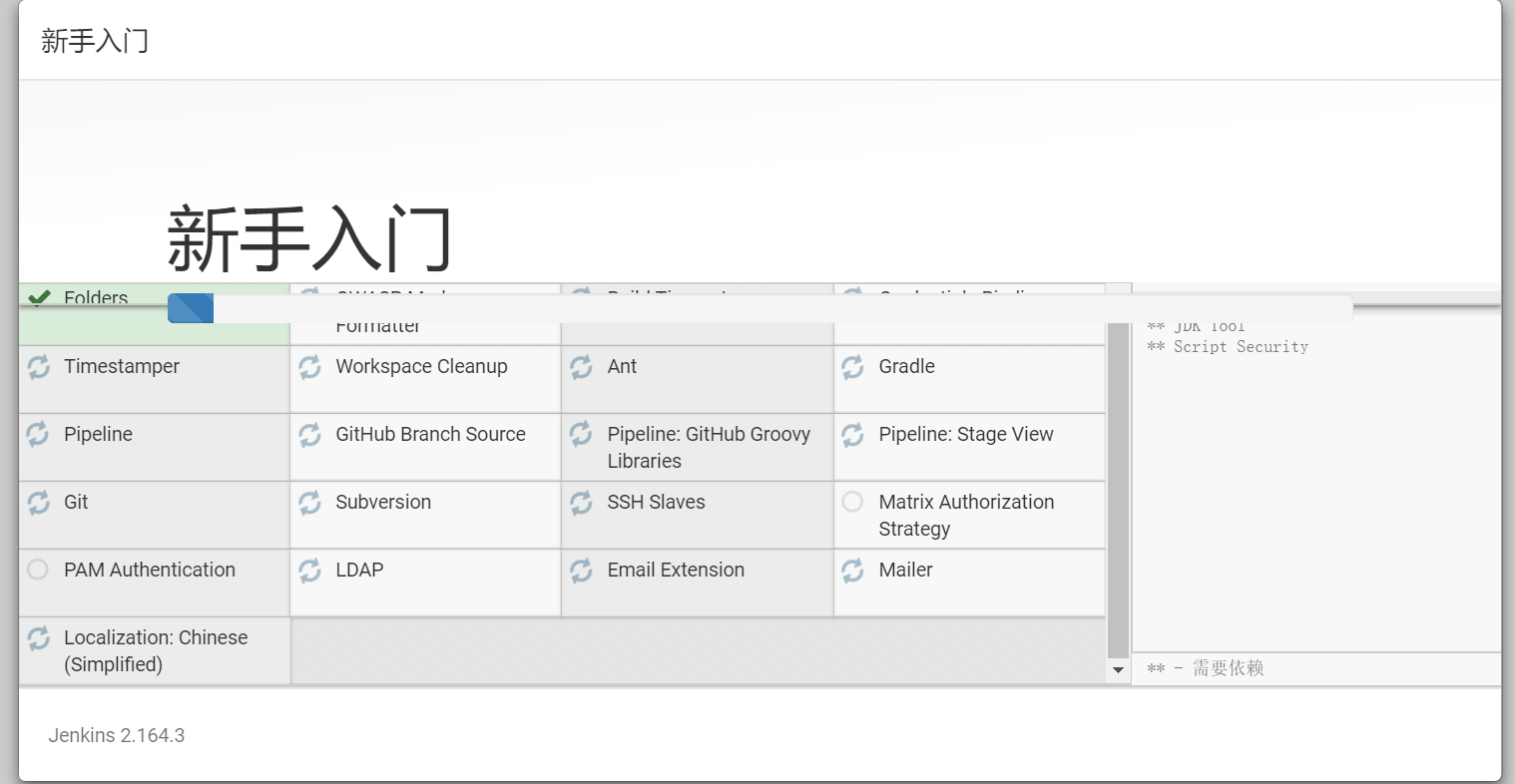
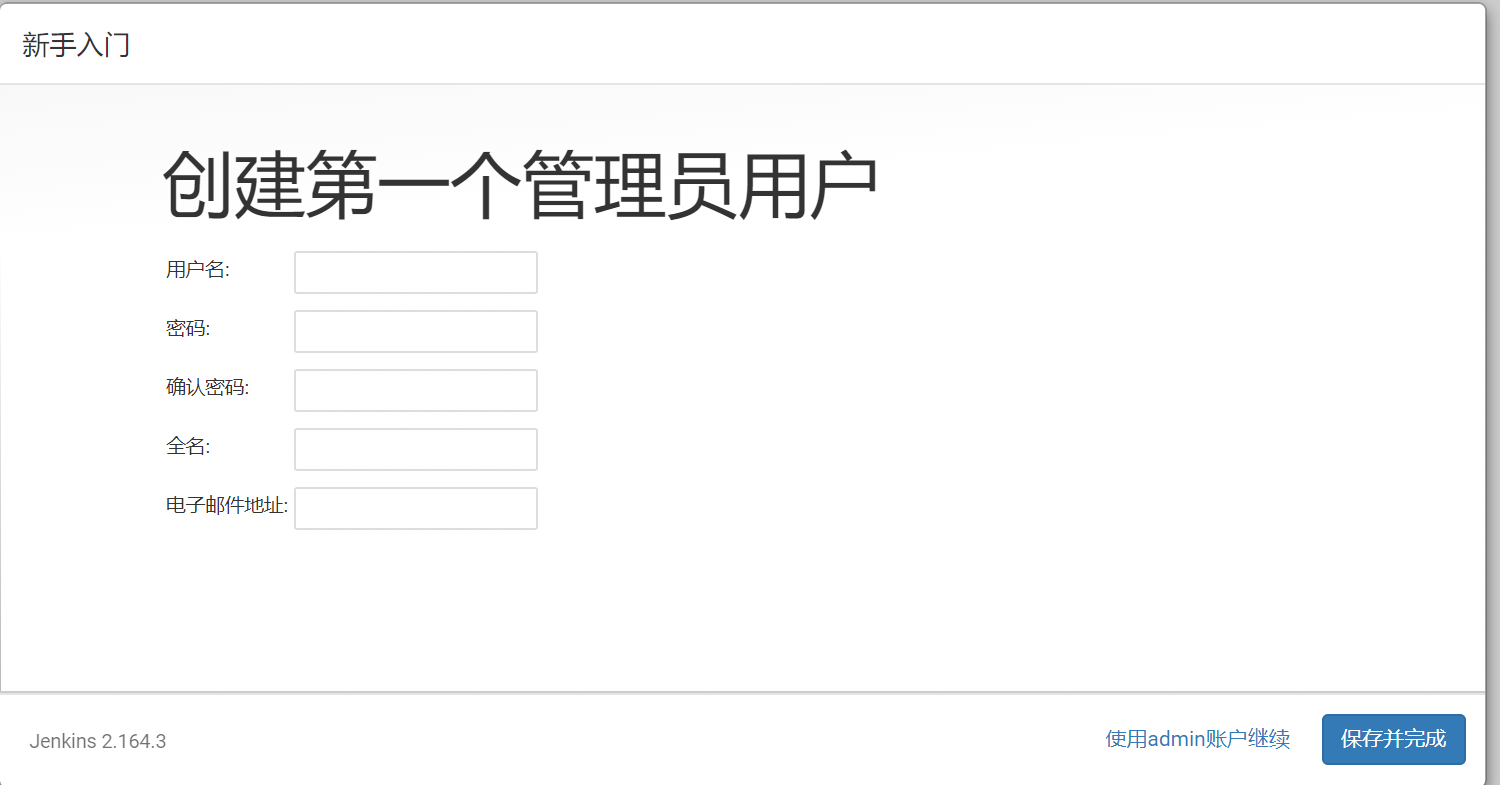
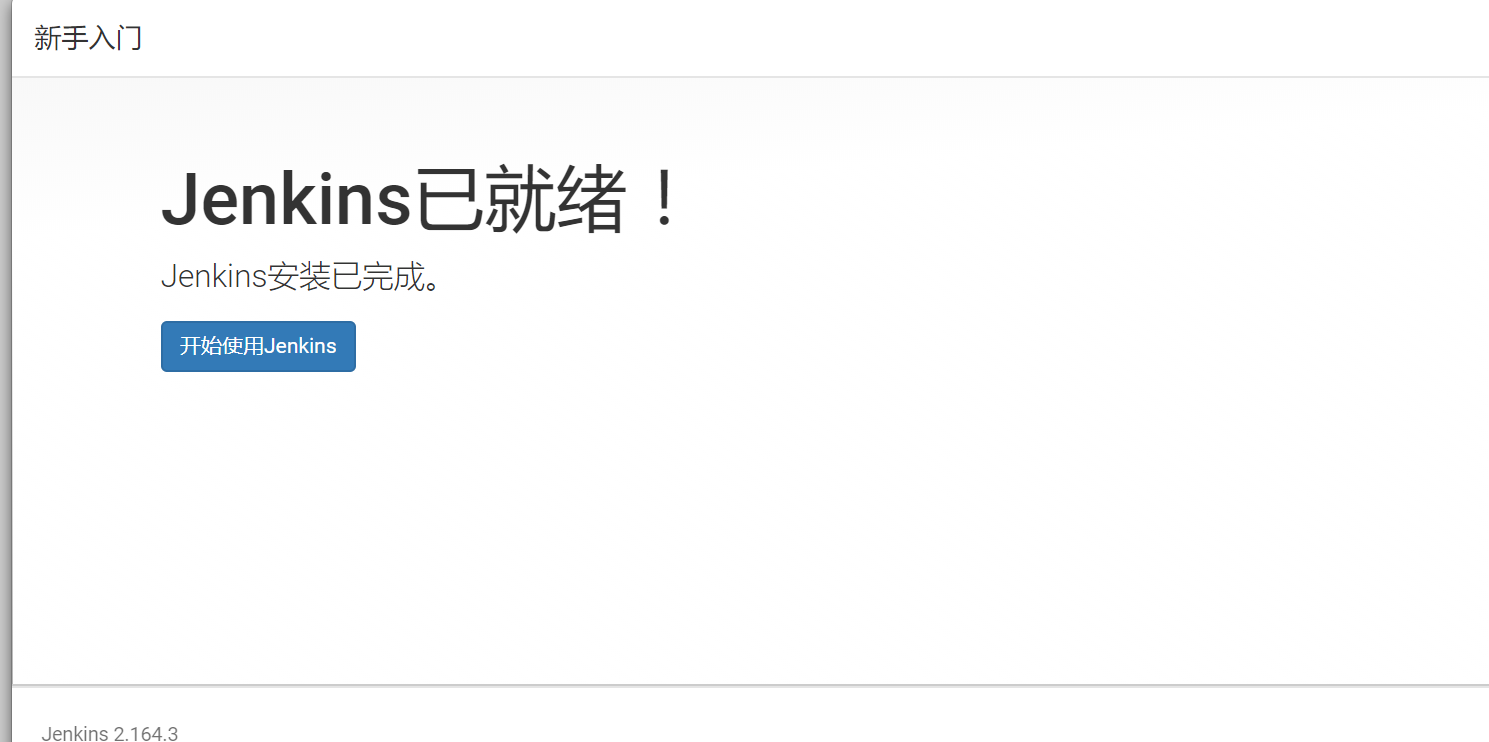
Jenkins系列之Jenkins的安装(一)的更多相关文章
- Jenkins系列之Jenkins的安装
我们在进行自动化测试的时候通常我们都会进行持续集成,可以帮助我们持续集成的工具有很多,我个人比较喜欢用Jenkins. 主要是因为它有如下优点: 开源免费 跨平台,支持所有的平台 web形式的可视化的 ...
- jenkins系列之jenkins job
第一步:在 jenkins 左边栏点击 "新建", 输入 job 名称,选择 "构建一个自由风格的软件项目" 一项.点击 "OK" . 第二 ...
- Jenkins系列之Jenkins配置常用工具和如何下载插件
上一篇我们介绍了Jenkins的安装,这一篇我们介绍如何配置Jenkins的工具和如何下载插件. 首先我们先来看如何配置工具,这里的工具是指JDK.Ant.Maven.Git等. 1.点击系统管理,如 ...
- Jenkins系列之Jenkins的工具配置和插件(二)
上一篇我们介绍了Jenkins的安装,这一篇我们介绍如何配置Jenkins的工具和如何下载插件. 首先我们先来看如何配置工具,这里的工具是指JDK.Ant.Maven.Git等. 一.如图,点击系统管 ...
- Jenkins持续集成企业实战系列之Jenkins持续集成简介及安装-----02
1. Jenkins持续集成简介 注:原创作品,允许转载,转载时请务必以超链接形式标明文章 原始出处 .作者信息和本声明.否则将追究法律责任. 最初接触Jenkins也是由于公司需求, ...
- jenkins入门系列之一 jenkins的安装
Jenkins是一个CI(持续集成环境)工具.它可以根据设定持续定期编译,运行相应代码:运行UT或集成测试:将运行结果发送至邮件,或展示成报告... 这样做的最终目的是: 让项目保持健康的状态.如果任 ...
- Jenkins系列之二——centos 6.9 + JenKins 安装
centos 6.9 + JenKins 安装记录环境: [root@localhost ~]# cat /etc/issue CentOS release 6.9 (Final) Kernel \r ...
- Jenkins持续集成企业实战系列之Jenkins插件下载及邮件配置-----05
注:原创作品,允许转载,转载时请务必以超链接形式标明文章 原始出处 .作者信息和本声明.否则将追究法律责任. 最初接触Jenkins也是由于公司需求,根据公司需求Java代码项目升级的.(公司是 ...
- Jenkins持续集成企业实战系列之Jenkins手动构建-----04
注:原创作品,允许转载,转载时请务必以超链接形式标明文章 原始出处 .作者信息和本声明.否则将追究法律责任. 最初接触Jenkins也是由于公司需求,根据公司需求Java代码项目升级的.(公司是 ...
随机推荐
- js类继承扩展super
相应的资料https://developer.mozilla.org/zh-CN/docs/Web/JavaScript/Reference/Operators/super 例子: class Pol ...
- 浅析分布式数据库中间件DDM
前言 DDM是什么?这是华为云Paas推出的分布式数据库中间件,DDM(Distributed Database Middleware)是一个实现了Mysql协议栈的服务器,前端用户可以把它看做一个数 ...
- opencv对图像进行边缘及角点检測
opencv对图像进行边缘及角点检測 先看结果: 代码: // ConsoleApplication1_812.cpp : Defines the entry point for the consol ...
- Proxy authentication confirmation prompt keeps popping up although the user/password is saved 火狐浏览器一直提示输入代理的账号和密码
https://support.mozilla.org/zh-CN/questions/943488 signon.autologin.proxy;true network.proxy.share_p ...
- CF 1042 A Benches —— 二分答案(水题)
题目:http://codeforces.com/problemset/problem/1042/A 代码如下: #include<iostream> #include<cstdio ...
- C#面向过程之局部变量、成员变量、变量作用域、可变参数
局部变量与成员变量: 局部变量:定义在方法里面的变量就叫做局部变量:没有默认的初始值,使用变量之前必须给它赋值成员变量:定义在类下面的变量叫做成员变量:如果是数值类型默认初始值为0 如果是引用类型默 ...
- 1章 SpringBoot介绍
新建一个SpringBoot版的Hello World.
- “ResGen.exe”已退出,代码为 -1073741701 或 “ResGen.exe”已退出,代码为 2。
解决的办法如下: 1.关闭所有Visual Studio: 2.以管理员的身份打开命令提示窗口:(开始-运行-cmd) 3.更改目录至"CD C:\Program Files (x86)\M ...
- samba - linux客户端访问samba服务器的指令(转载)
转自:http://linux.sheup.com/linux/linux5303.htm linux客户端访问samba服务器的指令2004-04-23 15:18 pm来自:Linux文档现载:W ...
- bzoj 1677: [Usaco2005 Jan]Sumsets 求和【dp】
设f[i]为i的方案数,f[1]=1,考虑转移,如果是奇数,那么就是f[i]=f[i-1]因为这1一定要加:否则f[i]=f[i-1]+f[i>>1],就是上一位+1或者i/2位所有因子乘 ...
