BZOJ 3884 拓展欧拉定理

3884: 上帝与集合的正确用法

Time Limit: 5 Sec  Memory Limit: 128 MB
Submit: 4142  Solved: 1907
[Submit][Status][Discuss]

Description

 

根据一些书上的记载，上帝的一次失败的创世经历是这样的：

第一天， 上帝创造了一个世界的基本元素，称做“元”。

第二天， 上帝创造了一个新的元素，称作“α”。“α”被定义为“元”构成的集合。容易发现，一共有两种不同的“α”。

第三天， 上帝又创造了一个新的元素，称作“β”。“β”被定义为“α”构成的集合。容易发现，一共有四种不同的“β”。

第四天， 上帝创造了新的元素“γ”，“γ”被定义为“β”的集合。显然，一共会有16种不同的“γ”。

如果按照这样下去，上帝创造的第四种元素将会有65536种，第五种元素将会有2^65536种。这将会是一个天文数字。

然而，上帝并没有预料到元素种类数的增长是如此的迅速。他想要让世界的元素丰富起来，因此，日复一日，年复一年，他重复地创造着新的元素……

然而不久，当上帝创造出最后一种元素“θ”时，他发现这世界的元素实在是太多了，以致于世界的容量不足，无法承受。因此在这一天，上帝毁灭了世界。

至今，上帝仍记得那次失败的创世经历，现在他想问问你，他最后一次创造的元素“θ”一共有多少种？

上帝觉得这个数字可能过于巨大而无法表示出来，因此你只需要回答这个数对p取模后的值即可。

你可以认为上帝从“α”到“θ”一共创造了10^9次元素，或10^18次，或者干脆∞次。

 

一句话题意：

Input

 

接下来T行，每行一个正整数p，代表你需要取模的值

Output

T行，每行一个正整数，为答案对p取模后的值

Sample Input

3
2
3
6

Sample Output

0
1
4

HINT

对于100%的数据，T<=1000,p<=10^7

---

欧拉定理 

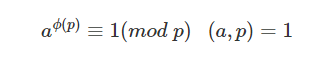    (a , p)  互质

拓展欧拉定理(降幂)

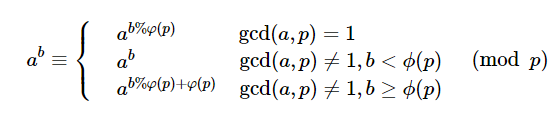 第二个式子不能合并到第三个

定理证明 不会..

---

解析   由于是2的无限次幂 所以每一层指数肯定大于对应的p   所以直接拓展欧拉定理第三个公式 递归求解phi(phi(phi(...))))  直到等于1  回朔的时候快速幂求解

复杂度 O(T*log(p)*sqtr(p)) 看起来很大 但是实际上上界是很松的，反正过了。据说打表会超时。

#include <bits/stdc++.h>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define all(a) (a).begin(), (a).end()
#define fillchar(a, x) memset(a, x, sizeof(a))
#define huan printf("\n");
using namespace std;
typedef long long ll;
const int maxn=1e5+,maxm=,inf=0x3f3f3f3f;
ll poww(ll n,ll m,ll mod)
{
    ll ans = ;
    while(m > )
    {
        if(m & )ans = (ans * n) % mod;
        m = m >> ;
        n = (n * n) % mod;
    }
    return ans;
}
ll phi(ll n)  //返回euler(n)
{
    ll res=n,a=n;
    for(ll i=; i*i<=a; i++)
    {
        if(a%i==)
        {
            res=res/i*(i-);//先进行除法是为了防止中间数据的溢出 爆int
            while(a%i==)
                a/=i;
        }
    }
    if(a>)
        res=res/a*(a-);
    return res;
}
ll dfs(ll p)
{
    if(p==)return ;
    ll x=phi(p);
    return poww(,dfs(x)+x,p);
}
int main()
{
    int t,p;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&p);
        printf("%lld\n",dfs(p));
    }
}