codeforces 880E. Maximum Subsequence(折半搜索+双指针)

E. Maximum Subsequence

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given an array a consisting of n integers, and additionally an integer m. You have to choose some sequence of indicesb1, b2, ..., bk (1 ≤ b1 < b2 < ... < bk ≤ n) in such a way that the value of 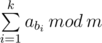 is maximized. Chosen sequence can be empty.

Print the maximum possible value of .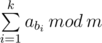

Input

The first line contains two integers n and m (1 ≤ n ≤ 35, 1 ≤ m ≤ 109).

The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109).

Output

Print the maximum possible value of .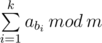

Examples

input

Copy

4 4
5 2 4 1

output

Copy

3

input

Copy

3 20
199 41 299

output

Copy

19

Note

In the first example you can choose a sequence b = {1, 2}, so the sum 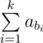 is equal to 7 (and that's 3 after taking it modulo 4).

In the second example you can choose a sequence b = {3}.

/*
折半搜索，把取模后的和存起来
双指针统计答案
*/
#include<bits/stdc++.h>

#define N 300000

using namespace std;
int a[N],p[N],q[N];
int k,t,ans,n,m,b,dep,flag;

inline int max(int x,int y){return x>y? x:y;}

inline int read()
{
    int x=,f=;char c=getchar();
    while(c>''||c<''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}

void dfs(int now,int sum)
{
    if(now==dep)
    {
        if(!flag)
        {
            p[++k]=sum,p[++k]=(sum+a[b])%m;return;
        }
        else
        {
            q[++t]=sum,q[++t]=(sum+a[n])%m;
            return ;
        }
    }
    dfs(now+,sum);
    dfs(now+,(sum+a[now])%m);
}

int main()
{
    n=read(),m=read(),b=n>>;dep=b;
    for(int i=; i<=n; ++i) a[i]=read();
    if(n==) printf("%d",a[]%m),exit();
    flag=;dfs(,);
    dep=n;flag=;dfs(b+,);
    int L=,R=t;
    sort(p+,p+k+);sort(q+,q+t+);
    while(L<=k)
    {
        while(p[L]+q[R]>=m) --R;
        ans=max(ans,p[L]+q[R]),++L;
    }
    ans=max(ans,p[k]+q[t]-m);
    printf("%d",ans);
    return ;
}