负载均衡算法，轮询方式 大话设计模式之工厂模式 C#

负载均衡算法，轮询方式

2018-04-13 17:37 by 天才卧龙, 13 阅读, 0 评论, 收藏, 编辑

学无止境，精益求精

十年河东，十年河西，莫欺少年穷

学历代表你的过去，能力代表你的现在，学习代表你的将来

首先说下这个算法的背景：

假设公司需要存储的信息量非常非常大而且访问量也是非常非常滴大（例如淘宝，天猫，京东等数据存储量和访问量都很大）

就拿天猫来举例：

马云：小陈啊，最近公司业务发展，数据存储量及访问量灰常灰常大，为减轻服务器的负载，限你们技术部提出一个解决方案？

小陈：马大帅，你一个当老师的瞎操心什么技术（不屑的眼神）

马云：你知道杭州电子科技大学吗？

小陈：一脸懵逼...

马云：这所学校的前身是杭州师范学院 ~_~ 注：（马云从杭州师范学院外国语系英语专业毕业）

小陈：马大帅您竟然是电子科技大的高材生，佩服佩服。我马上召集技术部人员，集思广益。~_~ 注：（小陈并不知道马云英语专业毕业）

半小时后小陈提出了解决方案：负载均衡

要想做到负载均衡，就必须写一套负载均衡算法：

在介绍负载均衡算法之前，我们来介绍下负载均衡的使用场景，如下：

还是以阿里巴巴天猫举例：假设天猫只有一台数据库服务器，随着数据存储量及访问量的直线式增加，这台服务器的吞吐量达到了极值，造成了访问速度越来越慢。马总看到眼里，急在心里！于是就有了上述的对话！

小陈提出的负载均衡是怎么一回事呢？

把原来的一台服务器扩充至几十台或者几百台服务器，当第一台服务器吞吐量高时，将用户的请求转向第二台服务器。同理，当第二台服务器的吞吐量高时，将用户的请求转向第三台服务器，以此类推...

那么，如果自动做到负载均衡呢？这里就需要负载均衡的算法了！

假设：天猫总共有数据库服务器四台，每台服务器的性能不同，第一台可提供的最大连接数为2，第二台服务器可提供的最大连接数为4，第三台服务器可提供的最大连接数为8，最后一台为12

假设：现在可用的服务器为第三台和第四台。

负载均衡算法如下：

namespace SJMS.test
{
    public class Test
    {
        static int maxLinkCount;
        //
        private static object lockHelper = new object();
        /// <summary>
        /// 所有快照/服务器的权重列表 所谓权重我们可理解为最大连接数
        /// </summary>
        static List<int> snapWeightList = new List<int>() { 2,4,8,12};

        //可用的服务器权重列表
        static List<int> EnableWeightList = new List<int>() { 8,12 };
        /// <summary>
        /// 当前的快照索引和权重信息
        /// </summary>
        static int curentSnapIndex, currentWeight, EnableWeight;
        /// <summary>
        /// 快照权重列表中最大的权重值和最大公约数
        /// </summary>
        static int maxWeight, gcd;

        static Test()
        {
            curentSnapIndex = -1;
            currentWeight = 0;
            EnableWeight = 0;
            maxWeight = GetMaxWeight(snapWeightList);
            EnableWeight = GetMaxWeight(EnableWeightList);
            gcd = GCD(snapWeightList);
            maxLinkCount = EnableWeightList.Sum();
        }
        /// <summary>
        /// 获取最大值 权重
        /// </summary>
        /// <param name="snapWeightList"></param>
        /// <returns></returns>
        public static int GetMaxWeight(List<int> snapWeightList)
        {
            int maxWeight = 0;
            foreach (int snapWeight in snapWeightList)
            {
                if (maxWeight < snapWeight)
                    maxWeight = snapWeight;
            }
            return maxWeight;
        }

        /// <summary>
        /// 获取最大公约数
        /// </summary>
        /// <param name="snapWeightList"></param>
        /// <returns></returns>
        public static int GCD(List<int> snapWeightList)
        {
            // 排序，得到数字中最小的一个
            snapWeightList.Sort(new WeightCompare());
            int minNum = snapWeightList[0];

            // 最大公约数肯定大于等于1，且小于等于最小的那个数。
            // 依次整除，如果余数全部为0说明是一个约数，直到打出最大的那个约数
            int gcd = 1;
            for (int i = 1; i <= minNum; i++)
            {
                bool isFound = true;
                foreach (int snapWeight in snapWeightList)
                {
                    if (snapWeight % i != 0)
                    {
                        isFound = false;
                        break;
                    }
                }
                if (isFound)
                    gcd = i;
            }
            return gcd;
        }

        /// <summary>
        /// 权重轮询调度算法/负载均衡算法
        /// </summary>
        public static int RoundRobinScheduling()
        {
            lock (lockHelper)
            {
                while (true)
                {
                    curentSnapIndex = (curentSnapIndex + 1) % EnableWeightList.Count;
                    if (curentSnapIndex == 0)
                    {
                        currentWeight = currentWeight - gcd;
                        if (currentWeight <= 0)
                        {
                            currentWeight = maxWeight;
                            if (currentWeight == 0)
                                return -1;
                        }
                    }
                    int A = snapWeightList[curentSnapIndex];
                    if (A >= currentWeight)
                    {
                        return EnableWeightList[curentSnapIndex];
                    }
                }
            }
        }
    }

    public class WeightCompare : System.Collections.Generic.IComparer<int>
    {
        public int Compare(int weightA, int weightB)
        {
            return weightA - weightB;
        }
    }

    public class DbSnapInfo
    {
        public int SouceID { get; set; }
        public bool Enable { get; set; }
        public int Weight { get; set; }
    }
}

这段代码有个比较难理解的地方：最大公约数的使用！（只可意会不可言传）

要想弄清楚最大公约数的使用，建议大家多次调试（调试时：变更服务器及服务器连接数）。

总之：算法的结果是帮你找到一个可用的服务器连接！

@陈卧龙的博客

大话设计模式之工厂模式 C#

2018-04-12 15:36 by 天才卧龙, 19 阅读, 0 评论, 收藏, 编辑

学无止境，精益求精

十年河东，十年河西，莫欺少年穷

学历代表你的过去，能力代表你的现在，学习代表你的将来

大话设计模式一书中第一个开讲的设计模式是简单工厂模式，关于简单工厂模式大家可参考鄙人的博客：代码无错就是优？简单工厂模式 C#

当然，本篇博客所讲的工厂模式和简单工厂模式还是非常类似的，因此，在进行工厂模式讲解之前，我们有必要重温下简单工厂模式

何为工厂模式？不论是简单工厂模式还是本篇的工厂模式，其工厂类主要负责生产对象，然后通过相应的对象调用相关的方法

在重温简单工厂模式之前，我们再次看下简单工厂模式的UML类图

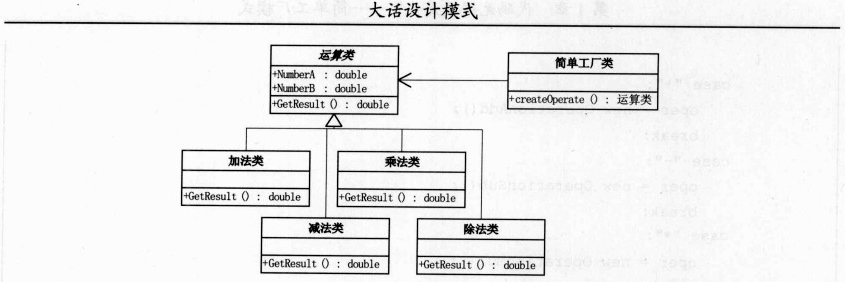
针对上述的简单工厂模式UML类图，我们得到如下叙述：

1、简单工厂类是和运算类是有关联的（实线加箭头代表关联），简单工厂类的主要功能是生产运算对象

2、运算类用斜体表示，说明运算类为抽象类，运算类有两个属性及一个返回值为 double 的方法

3、加减乘除类继承运算类并实现GetResult()方法。

针对上述三点叙述，我们可用如下代码来实现（如果你还看不懂UML类图，可以参考鄙人博客：UML类图应该怎么看？）

    public class 简单工厂类
    {
        double NumberA, NumberB;
        public 简单工厂类() { }
        public 简单工厂类(double A, double B)
        {
            this.NumberA = A;
            this.NumberB = B;
        }
        double Oper = new double();
        public double Operate(string 符号)
        {
            switch (符号)
            {
                case "+": Oper = new 加法类().GetResult(NumberA, NumberB); break;
                case "-": Oper = new 减法类().GetResult(NumberA, NumberB); break;
                case "*": Oper = new 乘法类().GetResult(NumberA, NumberB); break;
                case "/": Oper = new 除法类().GetResult(NumberA, NumberB); break;
            }
            return Oper;
        }
    }

    public abstract class 运算类
    {
        public abstract double GetResult(double NumberA, double NumberB);
    }

    public class 加法类:运算类
    {
        public override double GetResult(double NumberA, double NumberB)
        {
            return NumberA + NumberB;
        }
    }

    public class 减法类 : 运算类
    {
        public override double GetResult(double NumberA, double NumberB)
        {
            return NumberA - NumberB;
        }
    }

    public class 乘法类 : 运算类
    {
        public override double GetResult(double NumberA, double NumberB)
        {
            return NumberA * NumberB;
        }
    }

    public class 除法类 : 运算类
    {
        public override double GetResult(double NumberA, double NumberB)
        {
            if (NumberB != 0)
                return NumberA / NumberB;
            else throw new Exception("被除数不能为零");

        }
    }

        static void Main(string[] args)
        {
            double A = 1;
            double B = 2;
            string F = "/";
            简单工厂类 M = new 简单工厂类(A,B);
            double Result =  M.Operate(F);
            Console.WriteLine(Result);
            Console.ReadKey();
        }

上述代码是鄙人看着UML类图自己设计的，和博客：代码无错就是优？简单工厂模式 C# 中的设计代码并不一样！当然，这两种代码都准确的表达的简单工厂的理念。有兴趣的也可以看下 代码无错就是优？简单工厂模式 中的代码实现形式。

OK，上述就是简单工厂模式的代码设计方案！

但是简单工厂模式违反了设计模式的开闭原则，所以我们有必要对其进一步优化！

所谓开闭原则：

这个原则其实有两个特性，一个是说对于扩展是开放的，另一个是说，对于修改是封闭的（ASD原则）

如何优化呢？

工厂模式闪亮登场...

首先看下工厂模式关于加减乘除的UML类图

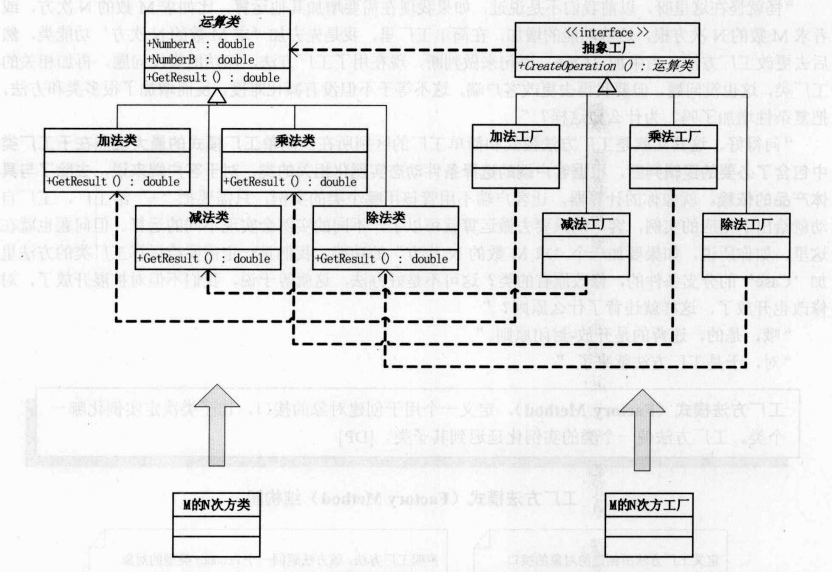
额，似乎复杂了很多！

不急，我们慢慢分析，然后再用代码实现！

1、运算工厂接口依赖运算类，加法工厂类依赖加法类，减法工厂类依赖减法类，乘法工厂类依赖乘法类，除法工厂类依赖除法类！（虚线加箭头代表依赖）

2、加减乘除工厂类继承运算工厂接口，加减成熟类继承运算类（三角加实线代表继承）

3、下方的M的N次方类和对应的工厂类是用来扩展的。

那么，分析了UML类图的信息，怎样用代码实现呢？

首先我们来创建左侧部分的五个类（运算类及加减乘除类），如下：

    /// <summary>
    /// 运算类
    /// </summary>
    public class Operation
    {
        public double NumberA, NumberB;
        public virtual double GetResult()
        {
            return 0;
        }
    }

    public class Add : Operation
    {
        public override double GetResult()
        {
            return NumberA + NumberB;
        }
    }

    public class Sub : Operation
    {
        public override double GetResult()
        {
            return NumberA - NumberB;
        }
    }

    public class Mul : Operation
    {
        public override double GetResult()
        {
            return NumberA * NumberB;
        }
    }

    public class Div : Operation
    {
        public override double GetResult()
        {
            if (NumberB == 0)
                throw new Exception("被除数不能为零");
            return NumberA / NumberB;
        }
    }

其次，我们来构建右侧部分的一个接口及四个类（加减乘除工厂类），如下：

    public interface IFactory
    {
        Operation GetOperation();
    }

    public class AddFactory : IFactory
    {
        public Operation GetOperation()
        {
            return new Add();
        }
    }

    public class SubFactory : IFactory
    {
        public Operation GetOperation()
        {
            return new Sub();
        }
    }

    public class MulFactory : IFactory
    {
        public Operation GetOperation()
        {
            return new Mul();
        }
    }

    public class DivFactory : IFactory
    {
        public Operation GetOperation()
        {
            return new Div();
        }
    }

客户端代码为：

        static void Main(string[] args)
        {
            IFactory F = new AddFactory();
            Operation AM = F.GetOperation();
            AM.NumberA = 8;
            AM.NumberB = 7;
            double sum = AM.GetResult();
            Console.WriteLine(sum);
            Console.ReadKey();
        }

最后，我们来运行一下（7+8=15）：

写到这儿，我可以自豪的说：如果你要加平方根运算，我只需新增平方根类及平方根工厂。因此，现在的设计是不违反设计模式的开闭规则的！

我们知道，在简单工厂模式中，我们可以通过运工厂类的 Switch Case 来判断具体的运算类型，但是上述所写的工厂模式却做不到了！这样写无形中加重了客户端的负担（客户端必须自己来判断运算类型），因此：有没有好的办法解决这个弊端呢？

答案是有，而且还有一个有趣的名字，叫：雷锋工厂

如何用代码实现呢？

@陈卧龙的博客