题解报告：hihoCoder #1175：拓扑排序·二

描述

小Hi和小Ho所在学校的校园网被黑客入侵并投放了病毒。这事在校内BBS上立刻引起了大家的讨论，当然小Hi和小Ho也参与到了其中。从大家各自了解的情况中，小Hi和小Ho整理得到了以下的信息：

校园网主干是由N个节点(编号1..N)组成，这些节点之间有一些单向的网路连接。若存在一条网路连接(u,v)链接了节点u和节点v，则节点u可以向节点v发送信息，但是节点v不能通过该链接向节点u发送信息。
在刚感染病毒时，校园网立刻切断了一些网络链接，恰好使得剩下网络连接不存在环，避免了节点被反复感染。也就是说从节点i扩散出的病毒，一定不会再回到节点i。
当1个病毒感染了节点后，它并不会检查这个节点是否被感染，而是直接将自身的拷贝向所有邻居节点发送，它自身则会留在当前节点。所以一个节点有可能存在多个病毒。
现在已经知道黑客在一开始在K个节点上分别投放了一个病毒。

举个例子，假设切断部分网络连接后学校网络如下图所示，由4个节点和4条链接构成。最开始只有节点1上有病毒。

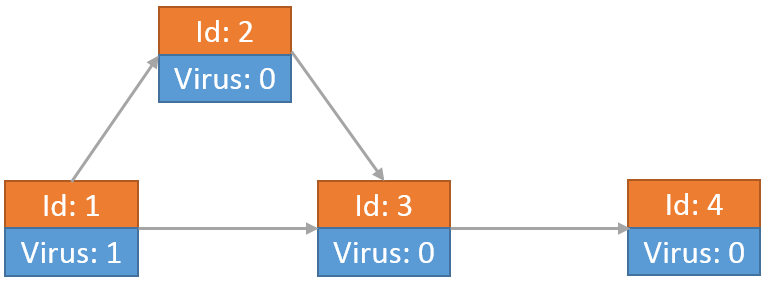
最开始节点1向节点2和节点3传送了病毒，自身留有1个病毒：

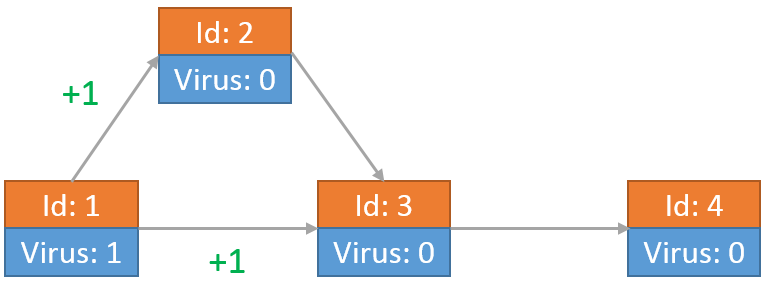
其中一个病毒到达节点2后，向节点3传送了一个病毒。另一个到达节点3的病毒向节点4发送自己的拷贝：

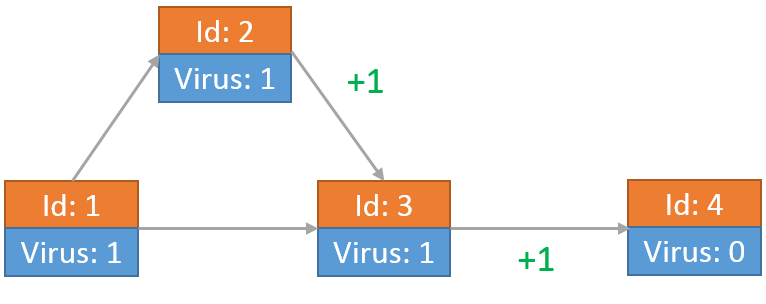
当从节点2传送到节点3的病毒到达之后，该病毒又发送了一份自己的拷贝向节点4。此时节点3上留有2个病毒：

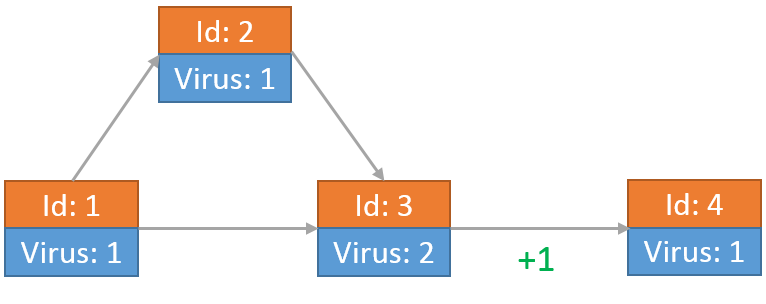
最后每个节点上的病毒为：

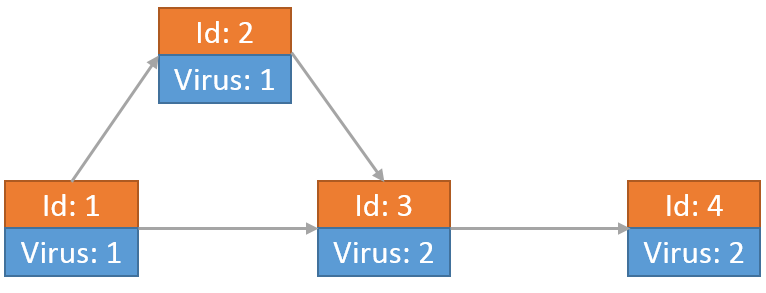
小Hi和小Ho根据目前的情况发现一段时间之后，所有的节点病毒数量一定不会再发生变化。那么对于整个网络来说，最后会有多少个病毒呢？

输入

第1行：3个整数N,M,K，1≤K≤N≤100,000，1≤M≤500,000

第2行：K个整数A[i]，A[i]表示黑客在节点A[i]上放了1个病毒。1≤A[i]≤N

第3..M+2行：每行2个整数 u,v，表示存在一条从节点u到节点v的网络链接。数据保证为无环图。1≤u,v≤N

输出

第1行：1个整数，表示最后整个网络的病毒数量 MOD 142857

样例输入

样例输出

6
解题思路：这道还是拓扑排序裸题，题目已经保证是有向无环图。要求每次出队队首元素，都要将本身所带病毒数传给其所有邻接点。最后计算所有节点编号的总病毒数。简单题，注意两数相加时要取余，避免数据溢出！
AC代码：

 #include<bits/stdc++.h>

 using namespace std;

 const int maxn=;

 const int mod=;

 vector<int> vec[maxn];//邻接表，每个节点保存与它相连的边的另一个端点

 queue<int> que;

 int n,m,k,x,u,v,InDeg[maxn],virus[maxn];//记录每个节点的入度，num用来表示节点的个数,virus数组用来记录每个节点的病毒个数

 void topsort(){

     for(int i=;i<=n;++i)

         if(!InDeg[i])que.push(i);//预处理，先将入度为0的节点编号入队

     while(!que.empty()){

         int now=que.front();que.pop();//出队入度为0的编号节点

         for(unsigned int i=;i<vec[now].size();++i){

             if(--InDeg[vec[now][i]]==)que.push(vec[now][i]);

             virus[vec[now][i]]=(virus[now]+virus[vec[now][i]])%mod;//注意取余操作，避免数据溢出

         }

     }

 }

 int main()

 {

     while(cin>>n>>m>>k){

         for(int i=;i<=n;++i)vec[i].clear();//全部清空

         memset(InDeg,,sizeof(InDeg));//全部顶点的度清0

         memset(virus,,sizeof(virus));

         while(k--){cin>>x;virus[x]++;}

         while(m--){

             cin>>u>>v;

             vec[u].push_back(v);//u指向v

             InDeg[v]++;//v的入度加1

         }

         topsort();

         int sum=;//保存所有节点病毒的总个数

         for(int i=;i<=n;++i)sum=(sum+virus[i])%mod;

         cout<<sum<<endl;

     }

     return ;

 }