matlab练习程序（点集配准的SVD法）

上一篇博客中我们使用了四元数法计算点集配准。

本篇我们使用SVD计算点集配准。

下面是《视觉slam十四讲》中的计算方法：

计算步骤如下：

我们看到，只要求出了两组点之间的旋转，平移是非常容易得到的，所以我们重点关注R的计算。展开关于R的误差项，得：

注意到第一项和R无关，第二项由于R'R=I，亦与R无关。因此，实际上优化目标函数变为：

接下来，我们介绍怎样通过SVD解出上述问题中最优的R，但关于最优性的证明较为复杂，感兴趣的读者请参考【50,51】，为了解R，先定义矩阵：

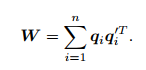
W是一个3*3的矩阵，对W进行SVD分解，得：

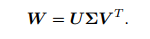
其中，为奇异值组成的对角矩阵，对角线元素从大到小排列，而U和V为正交矩阵，当W满秩时，R为：

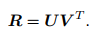
解得R后，按式7.53求解t即可。

具体证明可以参考：

代码如下：

clear all;
close all;
clc;

%生成原始点集
X=[];Y=[];Z=[];
for i=-::
    for j=-::
        x = i * pi / 180.0;
        y = j * pi / 180.0;
        X =[X,cos(y) * cos(x)];
        Y =[Y,sin(y) * cos(x)];
        Z =[Z,sin(x)];
    end
end
P=[X(:)' Y(1:3000)' Z(:)'];

%生成变换后点集
i=0.5;j=0.3;k=0.7;
Rx=[  ; cos(i) -sin(i);  sin(i) cos(i)];
Ry=[cos(j)  sin(j);  ;-sin(j)  cos(j)];
Rz=[cos(k) -sin(k) ;sin(k) cos(k) ;  ];
R=Rx*Ry*Rz;
X=P*R + [0.2,0.3,0.4];

plot3(P(:,),P(:,),P(:,),'b.');
hold on;
plot3(X(:,),X(:,),X(:,),'r.');

%计算点集均值
up = mean(P);
ux = mean(X);

P1=P-up;
X1=X-ux;

%计算点集协方差
sigma=P1'*X1/(length(X1));

[u s v] = svd(sigma);
RR=u*v';

%计算平移向量
qr=ux-up*RR;

%验证旋转矩阵与平移向量正确性
Pre = P*RR+qr;

figure;
plot3(P(:,),P(:,),P(:,),'b.');
hold on;
plot3(X(:,),X(:,),X(:,),'r.');
plot3(Pre(:,),Pre(:,),Pre(:,),'go');

处理效果和四元数法一致：

原始点集：

其中蓝点为原始点集，红点为旋转平移后的点集。

配准后点集：

计算得到的旋转平移矩阵，通过对蓝点集进行转换得到绿点集，比较红点集与绿点集是否基本一致。