条件随机场Conditional Random Field-CRF入门级理解

条件随机场Conditional Random Field-CRF入门级理解

 

有向图与无向图模型

CRF模型是一个无向概率图模型，更宽泛地说，它是一个概率图模型。现实世界的一些问题可以用概率图模型表示。这里可以用一个简单的例子说明：建立一个简单的图模型来分析一部电影是否会获得高票房。这个例子主要用于介绍概率图模型，其中的观点内容纯属编造。经过“认真”分析，发现一部电影的票房和以下因素有很大的关系：

• 剧本是否精彩，内容是否充实；
• 演员阵容是否强大，是否有可以吸引票房的明星；
• 演员表演是否精彩到位；
• 前期宣传是否到位；
• 上映时间是否合适，同期是否有其他实力强劲的电影；
• 投资。

上面的这些因素可以转化成一个个随机变量，将它们按照彼此之间的依赖关系进行连线，就得到了下图：

从模型图中可以很清晰看出每一个项目与电影票房之间的关系。拥有了这些关系，就可以根据其中一些变量推断出其他变量的情况。这里将每一个变量都离散化为2个等级——好和差，然后就可以根据分析得到的经验构建心目中的条件概率分布表，如下图所示：

有了这个图和对应的表格，整个概率图模型就变得十分明确，这个图模型可以帮助完成很多事情，读者可以使用它在概率图模型的小世界中完成各种各样的推断，例如：

计算联合概率（Joint Probability）。一个投资少、宣传弱、阵容弱、表演弱且票房好的电影出现的概率有多大？公式如下：

计算边际概率（Marginal Probability）。投资多，阵容强，票房好，其他无所谓的电影出现的概率有多大？公式如下：

计算条件概率（Conditional Probability）。当一个电影宣传强、阵容强、表演强、票房好时，它（竟然）投资少的概率有多大？公式如下：

可以看出，这些推断都可以通过上面的图模型很好地推断出来，为理解这个模型提供更多的帮助。以上是一个简单的概率图模型的例子。当然，上面这个模型是一个有向图模型，还不是CRF归属的无向图模型。

概率图模型主要由有向图和无向图两部分组成。那么无向图和有向图有什么区别呢？就是随机变量的依赖关系。方向有什么好处和坏处呢？有了方向，整个概率图中概率或者信念（belief）的流动方向就可以确定，就能知道一个个随机变量之间的依赖关系，例如在上面的例子中，好几个因素和投资都有依赖关系，所以在求解时，投资这个因素需要首先明确。

在有向图模型中，每一个随机变量都拥有自己的条件概率分布（Conditional Probablistic Distribution，CPD），这些随机变量的概率依赖于它的父辈随机变量的取值。这样的局部条件概率是很有用的，它使得计算联合概率和边际概率时变得比较容易。以上面的那些例子为例，在计算时我们只需要将这些CPD的取值连乘起来就可以了。

无向图因为没有方向，也就没有CPD，但是无向图模型还是有自己的办法。无向图模型中同样的一个个类似CPD的东西被称作Factor，像有向图中的节点拥有自己的CPD一样，Factor也有自己的表示形式。它也可以像CPD一样用表格的形式表示。

例如空间内有四个粒子，每个粒子都有两种状态，它们之间还存在着一定的相互影响关系，这个关系由Factor来就如下图所示：

从上面的例子可以看出，Factor和CPD相比有一个明显的不同。CPD中所有的概率和为1，而Factor里所有的条目-entry没有和且和并不为1。

和不为1并不是很好理解，概率的基本原则就是需要所有事件发生的概率和为1。当然这没有错，因为无向图的Factor表示的并不是条件概率，而是一种更为对称的亲密关系（affinities）。求解无向图的联合概率需要换一种方法，那就是把所有的Factor像有向图模型的贝叶斯网络那样都连乘起来，再进行归一化。

在上面的例子中，如果要求P(A=1，B=1，C=1，D=1)的概率，那么有：

上面的计算也可以用代码的形式进行计算：

这样就得到了所有的联合概率：

从代码中可以看出，没有了有向图的依赖，无向图少了很多约束，计算公式反而更简洁。当完成归一化后，这些计算结果就可以像有向图那样表示随机变量的联合概率。这些联合概率实际上代表了无向图模型的概率分布，这种分布被称为Gibbs分布 。Gibbs分布就是利用Factor表示的无向图模型的概率分布，它的形式如下所示：

实际上Gibbs分布的形式展示了利用无向图模型计算联合概率的过程。得到了联合概率，就可以计算边际概率和条件概率。通过上面的计算，无向图模型和有向图模型又走到同一起跑线。由于两者确实存在明显不同，因此两者的名字也有些不同，有向图网络一般被称为“贝叶斯网络”（Bayesian Network），而无向图网络一般被称为“马尔可夫随机场”（Markov Random Field）。

为什么会有无向图和有向图这两类图模型，两者能不能合二为一？实际上这两种模型有各自的应用领域，有向图模型虽然清晰简单，但它并不能表示所有的真实场景，有向图模型通常需要一个有顺序的推断过程，这里暗示了一些依赖关系和独立条件，而无向图模型由于没有方向，也就没那么多限制，所以无向图模型可以用来对更多更复杂的问题进行建模。但是放弃了方向，也就意味着放弃了条件依赖和一些条件独立的特性，于是只能用Factor的形式和Gibbs分布进行表示，表示形式有些复杂。

除了上述介绍的区别，Factor和CPD相比也有很大不同。因为没有和为1的限制，所以整体上看它对数值要求很宽松，但是它也有自己的坏处，那就是想从Factor的表格形式中读出一些有价值的信息是比较困难的，这个困难有两个方面：

首先，因为不具有和为1的限制，无向图模型的概率比较抽象。对比贝叶斯网络的CPD，就会发现CPD描述得更加清楚。

其次，由于Factor的依赖关系不明朗，表格中记述的一些关系和全局状态下的关系有时是相反的。当读者具体观察某个Factor时，会觉得某组随机变量比另外一组亲密度高，产生的概率一定更高；但是如果站在全局观察，把联合概率计算出来再去计算它们的边际概率，就会发生Factor内表述的关系和全局信息相反。CPD在这方面具有绝对优势，局部的条件概率放在全局还是合理的。

这里举一个例子，如果将上面的代码做一些改动，去求A、B的边际概率，就有：

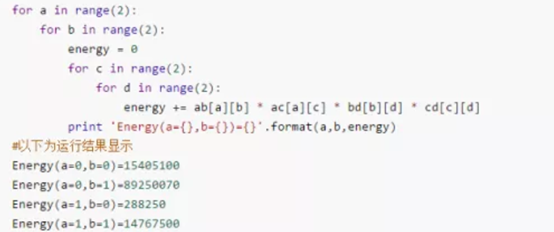
和A、B所在的Factor相比，Ф（A=1, B=1）在Factor中第二大，但是到了边际概率中它却成了第三大，说明从Factor中分析有时并不能看出某个事件的边际概率。

至此，概率图模型和有向无向图模型相关的基本内容就介绍完了。

Log-Linear Model

在了解无向图模型和Gibbs分布相关概念后，可以针对具体问题进行建模了，但是实际上，上述表格形式的模型并不好用。因为采用表格的形式去表达模型，需要将随机变量的所有取值形式都写出来，如果变量的取值范围不大还可以接受，如果取值范围非常大，那么这种表格形式对建模者来说就是个不小的负担，所以表示Factor形式需要改变。为了解决这个问题，Factor的形式需要被重新定义，首先需要把Factor函数转换成能量函数：

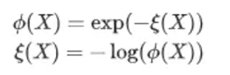
我们把Ф（X）称作Factor函数，把ξ（X）称作能量函数（Energy Function）。在物理学中，能量越大的物质存在的概率越小，能量越小的物质存在的概率越大。这个性质很符合函数的关系。这个函数带来了两个好处:

首先，Factor函数中的每一项表示了随机变量间的亲密关系，一般来说这个值是非负的，这个限制会对建模造成困扰，因此利用指数函数变换，现在的Energy函数摆脱了非负数的限制，变得可正可负。

另外还有一个十分重要的特性：原来的乘法关系变成了现在的加法关系。现在有:

变成加法关系后，建模求解都变得简单了不少，因为加法的关系更利于分析和计算。当然，模型形式变换到这一步还不够，想要得到进一步的化简，就要引入Feature这个概念。

我们已经了解了Factor的一般表现形式--表格的形式，但很多时候Factor的表格是比较稀疏的。虽然参与一个Factor的随机变量很多，但是真正有意义的亲密关系其实没几个。这样表格的形式就变得不再实用，Feature表示的形式更适合这种场景，那么Feature形式是什么样的呢？

举个例子，有一个由两个灰白像素随机变量组成的Factor，每个变量的取值范围为[0,255]的整数。如果用Factor表示，这个Table将会有256*256=65536个条目，但是如果这个Factor中表示的亲密关系和两个像素的值是否相等有关，像素值相等是关系为1，不相等为0，那么用Feature表示需要写成：

这种写法只要用两个条目就可以表述清楚。所以Feature就是通过尽可能地合并相同结果使Factor的表示变得简洁。以上就是Log-Linear模型的特点，可以看出它对无向图模型进行了极大的化简。未来的模型主要基于这一个框架进行构建。

条件随机场

条件随机场的全称是Conditional Random Field（CRF）。它是马尔可夫随机场的一种特殊形式。前面说到了马尔可夫随机场和联合概率分布之间的计算关系，这里的条件随机场则主要对应了条件概率分布。条件随机场中参与计算的有两部分随机变量—X和Y。一般来说X被称作观察变量，也就是已知的变量，Y被称作目标变量或者隐含变量，是需要通过模型求解的变量。CRF的出现与贝叶斯公式有关：

其中，P（X,Y）就是图模型的联合概率分布，而在有些问题中，对X单独建模十分困难，而对X,Y联合建模则相对容易些，这样的问题需要特殊的条件约束。条件随机场不允许任何一个Factor中只包含X的节点，Factor中要么包X和Y，要么只包含Y。于是上面的公式就可以做一定的修改，使得在建模时避免这些问题。这里给出一种相对简单的条件随机场，如下图所示：

它的形式如下所示：

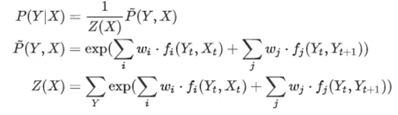
从图中可以观察出，它确实没有只包含X的Factor。模型的条件概率通过计算联合概率和边际概率得到，而边际概率又是通过联合概率得到，这样难以建模的边际概率就通过联合概率得到解决。

采用无向图模型建模的CRF具有很强的表达能力和灵活性，但是计算起来却不那么容易。所有的概率推断必须从求解联合概率入手，还要计算非常复杂归一化项，所以计算是无向图模型的一大难题。

学习来源：《深度学习轻松学》第九章—图像的语义分割，作者冯超