基于python的数学建模---分支定界算法

• zip函数

a = [1,2,3,4]
b = [5,6,7,8]
i = sum(x * y for x, y in zip(a, b))
print(i)
70

• floor and ceil 函数

import math

a = 34.3

print(math.floor(a))
print(math.ceil(a))

34
35

• all 函数

print(all([1,2,3,4,5]))
print(all([1,2,3,0,5]))

True
False

• enumerate 函数

seasons = ['Spring', 'Summer', 'Fall', 'Winter']
print(list(enumerate(seasons)))
[(0, 'Spring'), (1, 'Summer'), (2, 'Fall'), (3, 'Winter')]

• len 函数

A = [[1,2,3,4],[3,4,5,6]]
print(len(A))
2

• 分支代码
• 

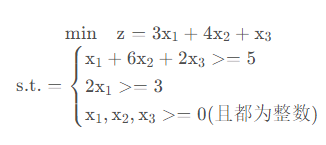
import math
from scipy.optimize import linprog
import sys

def integerPro(c, A, b, Aeq, beq, t=1.0E-8):
    res = linprog(c, A_ub=A, b_ub=b, A_eq=Aeq, b_eq=beq)
    bestVal = sys.maxsize  # 很大一个数
    bestX = res.x
    if not (type(res.x) is float or res.status != 0):
        bestVal = sum([x * y for x, y in zip(c, bestX)])
    if all(((x - math.floor(x)) <= t or (math.ceil(x) - x) <= t) for x in bestX):
        return bestVal, bestX
    else:
        ind = [i for i, x in enumerate(bestX) if (x - math.floor(x)) > t and (math.ceil(x) - x) > t][0]
        newCon1 = [0] * len(A[0])
        newCon2 = [0] * len(A[0])
        newCon1[ind] = -1
        newCon2[ind] = 1
        newA1 = A.copy()
        newA2 = A.copy()
        newA1.append(newCon1)
        newA2.append(newCon2)
        newB1 = b.copy()
        newB2 = b.copy()
        newB1.append(-math.ceil(bestX[ind]))
        newB2.append(math.floor(bestX[ind]))
        r1 = integerPro(c, newA1, newB1, Aeq, beq)
        r2 = integerPro(c, newA2, newB2, Aeq, beq)
        if r1[0] < r2[0]:
            return r1
        else:
            return r2

if __name__ == '__main__':

    c = [3, 4, 1]
    A = [[-1, -6, -2], [-2, 0, 0]]
    b = [-5, -3]
    Aeq = [[0, 0, 0]]
    beq = [0]
    print(integerPro(c, A, b, Aeq, beq))

(8.000000000001586, array([2.00000000e+00, 1.83247535e-13, 2.00000000e+00]))

8是目标函数值，array是变量值x1、x2、x3