Java解决LeetCode72题 Edit Distance

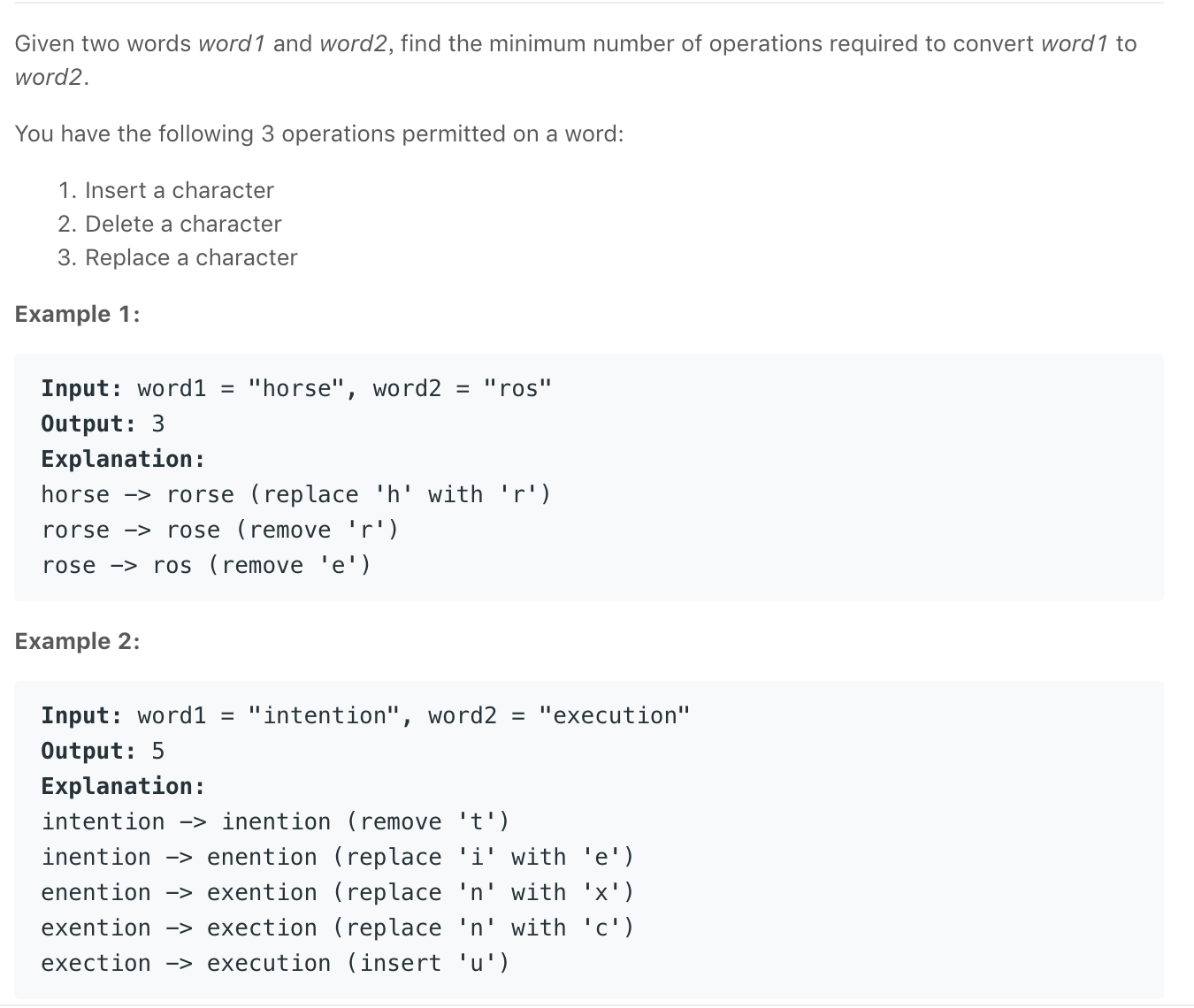
题目描述

地址 ： https://leetcode.com/problems/edit-distance/description/

思路

• 使用dp[i][j]用来表示word1的0~i-1、word2的0~j-1的最小编辑距离
• 我们可以知道边界情况：dp[i][0] = i、dp[0][j] = j，代表从 "" 变为 dp[0~i-1] 或 dp[0][0~j-1] 所需要的次数

同时对于两个字符串的子串，都能分为最后一个字符相等或者不等的情况：

• 如果word1[i-1] == word2[j-1]：dp[i][j] = dp[i-1][j-1]
• 如果word1[i-1] != word2[j-1]：
  • 向word1插入：dp[i][j] = dp[i][j-1] + 1
  • 从word1删除：dp[i][j] = dp[i-1][j] + 1
  • 替换word1元素：dp[i][j] = dp[i-1][j-1] + 1

 public int minDistance(String word1, String word2) {
    int n = word1.length();
    int m = word2.length();
    int[][] dp = new int[n + 1][m + 1];
    for (int i = 0; i < m + 1; i++) {
        dp[0][i] = i;
    }
    for (int i = 0; i < n + 1; i++) {
        dp[i][0] = i;
    }
    for (int i = 1; i < n + 1; i++) {
        for (int j = 1; j < m + 1; j++) {
            if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                dp[i][j] = dp[i - 1][j - 1];
            } else {
                dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
            }
        }
    }
    return dp[n][m];
}