poj 2284 That Nice Euler Circuit 解题报告

That Nice Euler Circuit

Time Limit: 3000MS		Memory Limit: 65536K
Total Submissions: 1975		Accepted: 624

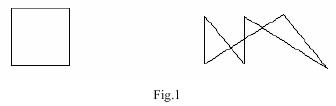
Description

Little Joey invented a scrabble machine that he called Euler, after the great mathematician. In his primary school Joey heard about the nice story of how Euler started the study about graphs. The problem in that story was - let me remind you - to draw a graph on a paper without lifting your pen, and finally return to the original position. Euler proved that you could do this if and only if the (planar) graph you created has the following two properties: (1) The graph is connected; and (2) Every vertex in the graph has even degree.

Joey's Euler machine works exactly like this. The device consists of a pencil touching the paper, and a control center issuing a sequence of instructions. The paper can be viewed as the infinite two-dimensional plane; that means you do not need to worry about if the pencil will ever go off the boundary.

In the beginning, the Euler machine will issue an instruction of the form (X0, Y0) which moves the pencil to some starting position (X0, Y0). Each subsequent instruction is also of the form (X', Y'), which means to move the pencil from the previous position to the new position (X', Y'), thus draw a line segment on the paper. You can be sure that the new position is different from the previous position for each instruction. At last, the Euler machine will always issue an instruction that move the pencil back to the starting position (X0, Y0). In addition, the Euler machine will definitely not draw any lines that overlay other lines already drawn. However, the lines may intersect.

After all the instructions are issued, there will be a nice picture on Joey's paper. You see, since the pencil is never lifted from the paper, the picture can be viewed as an Euler circuit.

Your job is to count how many pieces (connected areas) are created on the paper by those lines drawn by Euler.

Input

There are no more than 25 test cases. Ease case starts with a line containing an integer N >= 4, which is the number of instructions in the test case. The following N pairs of integers give the instructions and appear on a single line separated by single spaces. The first pair is the first instruction that gives the coordinates of the starting position. You may assume there are no more than 300 instructions in each test case, and all the integer coordinates are in the range (-300, 300). The input is terminated when N is 0.

Output

For each test case there will be one output line in the format

Case x: There are w pieces.,

where x is the serial number starting from 1.

Note: The figures below illustrate the two sample input cases. 

Sample Input

5
0 0 0 1 1 1 1 0 0 0
7
1 1 1 5 2 1 2 5 5 1 3 5 1 1
0

Sample Output

Case 1: There are 2 pieces.
Case 2: There are 5 pieces.

Source

Shanghai 2004

[Submit]   [Go Back]   [Status]   [Discuss]

Home Page   Go Back  To top

————————————————————我是分割线————————————————————————

绝世好题。

大体思路简单，细节能烦死人。

改了2天，看着题解才写出几个函数。55555........

本题根据平面图的欧拉定理求解区域个数r。

顶点个数：两两线段求交点，每个交点都是图中的顶点。

边数：在求交点时判断每个交点落在几条边上，若一个交点落在某条边上，则将这条边分裂成两条边，边数++。

之后运用欧拉定理求区域个数即可。

最后减的时候，把n处理成了点数，错的离谱......

 /*
     Problem:poj 2284
     OJ:     POJ
     User:   S.B.S.
     Time:   454 ms
     Memory: 3548 kb
     Length: 2643 b
 */
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<algorithm>
 #include<queue>
 #include<cstdlib>
 #include<iomanip>
 #include<cassert>
 #include<climits>
 #include<vector>
 #include<list>
 #include<map>
 #define maxn 90001
 #define F(i,j,k) for(int i=j;i<k;i++)
 #define M(a,b) memset(a,b,sizeof(a))
 #define FF(i,j,k) for(int i=j;i>=k;i--)
 #define inf 0x7fffffff
 #define maxm 2016
 #define mod 1000000007
 #define eps 1e-10
 //#define LOCAL
 using namespace std;
 int read(){
     int x=,f=;char ch=getchar();
     while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
     while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
     return x*f;
 }
 int n,m;
 struct POINT //点
 {
     double x;
     double y;
     POINT(double a=,double b=){x=a;y=b;}
 };
 struct EDGE //线段
 {
     POINT u;
     POINT v;
     EDGE(POINT A,POINT B) {u=A;v=B;}
 };
 struct LINE //直线
 {
     double a;
     double b;
     double c;
 };
 bool operator < (POINT A,POINT B)
 {
     return A.x<B.x || A.x==B.x && A.y<B.y;
 }
 bool operator == (POINT a,POINT b)
 {
     return abs(a.x-b.x)<eps && abs(a.y-b.y)<eps;
 }
 bool online(EDGE a,POINT b)
 {
     return abs((a.v.x-a.u.x)*(b.y-a.u.y)-(b.x-a.u.x)*(a.v.y-a.u.y))<eps && (b.x-a.u.x)*(b.x-a.v.x)<eps && (b.y-a.u.y)*(b.y-a.v.y)<eps;
 }
 LINE makeline(POINT a,POINT b)
 {//将线段延长成直线
     LINE l;
     l.a=(b.y>a.y) ? b.y-a.y : a.y-b.y;                //y方向差值
     l.b=(b.y>a.y) ? a.x-b.x : b.x-a.x;                //x方向差值
     l.c=(b.y>a.y) ? a.y*b.x-a.x*b.y : a.x*b.y-a.y*b.x;//与水平线夹角
     return l;    //返回直线
 }
 bool lcross(LINE a,LINE b,POINT &p)
 {//判断直线是否相交
     double d=a.a*b.b-b.a*a.b;
     if(abs(d)<eps) return false;
     //求交点
     p.x=(b.c*a.b-a.c*b.b)/d;
     p.y=(b.a*a.c-a.a*b.c)/d;
     return true;
 }
 bool ecross(EDGE a,EDGE b,POINT &p)
 {
     LINE l1,l2;
     l1=makeline(a.u,a.v);
     l2=makeline(b.u,b.v);
     if(lcross(l1,l2,p)) return online(a,p) && online(b,p);
     else return false;
 }
 POINT p[maxn],in[maxn];
 int cur,cnt,ans;
 int main()
 {
     std::ios::sync_with_stdio(false);//cout<<setiosflags(ios::fixed)<<setprecision(1)<<y;
     #ifdef LOCAL
     freopen("data.in","r",stdin);
     freopen("data.out","w",stdout);
     #endif
     int t=;
     while(cin>>n&&n)
     {
         t++;m=cur=;
         for(int i=;i<n;i++) cin>>p[i].x>>p[i].y;
         for(int i=;i<n;i++)
          for(int j=;j<n;j++){
             EDGE l1(p[i],p[(i+)%n]),l2(p[j],p[(j+)%n]);
             POINT pp;
             if(ecross(l1,l2,pp)) in[cur++]=pp;
         }
         sort(in,in+cur);
         cur=unique(in,in+cur)-in;
         for(int i=;i<cur;i++)
          for(int j=;j<n;j++){
             EDGE ll(p[j],p[(j+)%n]);
             if(online(ll,in[i]) && !(ll.u==in[i])) m++;
         }
         cout<<"Case "<<t<<": There are "<<+m-cur<<" pieces."<<endl;
     }
     return ;
 }

poj 2284