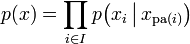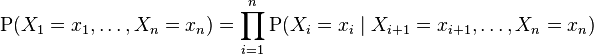PGM学习之二 PGM模型的分类与简介

废话：和上一次的文章确实隔了太久，希望趁暑期打酱油的时间，将之前学习的东西深入理解一下，同时尝试用Python写相关的机器学习代码。

一 PGM模型的分类

通过上一篇文章的介绍，相信大家对PGM的定义和大致应用场景有了粗略的了解。那么接下来我们来深入了解下PGM。

首先要介绍的是Probabilistic models（概率模型），常用来描述不同的随机变量之前的关系，主要针对变量或变量间的相互不确定性的概率关系建模。总的来说，概率模型分为两类：

一类是参数模型-可以用有限个参数进行准确定义

参数模型是一组由有限维参数构成的分布集合。其中 是参数，而是其可行欧几里得子空间。概率模型可被用来描述一组可产生已知采样数据的分布集合。例如，假设数据产生于唯一参数的高斯分布，则我们可假设该概率模型为。

二类是非参数模型-即无法采用有限参数进行准确定义的模型

无参数模型则是一组由无限维参数构成的概率分布函数集合，可被表示为。相比于无参数模型和参数模型，半参数模型也由无限维参数构成，但其在分布函数空间内并不紧密。例如，一组混叠的高斯模型。确切的说，如果是参数的维度，是数据点的大小，如果随着 和  则 ，则我们称之为半参数模型。

概率模型是所有数理统计问题的前提，选择合适的概率模型对于解决实际问题具有非常重要的意义。在选择模型时，需要考虑以下以及各因素：

1. 所研究的随机现象的基本概率特征, 例如: 对称性, 矩条件
2. 描述随机现象的随机变量是连续随机变量还是离散随机变量, 或者相关随机变量是否具有混合概率分布等复杂分布形式
3. 对于参数模型, 问题的参数分布族是具有什么形式, 参数空间的选择
4. 解决问题所要用到的统计量, 以及相应的假设检验方法

PGM即是概率模型的一种，通过利用有向图或者无向图来表示变量之前的概率关系，我们可以将复杂的概率模型转换为纯粹的代数运算。常见的PGM的分类如下图所示：

二 PGM模型中Factor的理解与运算

在进一步理解如此众多的PGM模型前，我们首先来回忆一下有关PGM中factors的知识。Factors可以叫做影响因子，在一个PGM模型中，一个Factor可以看做Graph中的一个节点；两个Factor之间的联系用图的边来表示。在PGM中，Factor是在高维空间中定义概率分布的基础和原子；在Factor上定义的操作是概率分布公式推导的基础。在由两个Factor构成的最简单的有向图的PGM模型里，Factor与概率的转化关系如下图所示：

简单的说，一个PGM模型最终可以建模表示成图中所有Factor的联合概率分布，然后根据Factor之间的运算规则，可以将该联合概率分布转化为可运算的概率分布的乘积。

如上图所示，Factor1有箭头指向Factor2，表示Factor1是Factor2的条件，那么P(Factor2)=P(Factor2|Factor1)。这种箭头表示的是Factor之间的联系，在有向图PGM模型中，若干个Factor和若干条箭头之间，Factor之间的相互影响，可以用Chain Rules（链式法则）来表示。那么接下来，我们来理解一下什么是Chain Rules。

上图中，P(G,D,I,S,L)是图右侧所示有向PGM模型的联合概率分布。在该模型中，Grade受Course Difficulty和Student Intelligence的影响；SAT受Student Intelligence的影响；Reference Letter受Grade的影响。

根据前述的运算规则，有：P(D,I,G,S,L)=P(D)*P(I)*P(G|I,D)*P(L|G)*P(S|I)，也就是说，PGM模型的所有因子的联合概率分布，等于各因子概率的乘积。那么，如何根据各因子的概率分布计算PGM模型所代表的联合概率分布呢？以最简单的离线分布为例：

图中给出了每一个因子的分布，同时我们还知道：P(D,I,G,S,L)=P(D)*P(I)*P(G|I,D)*P(L|G)*P(S|I)。接下来我们计算联合概率分布：

P(D=0,I=1,G=3,S=1,L=1)=P(D=0)*P(I=1)*P(G=3|I=1,D=0)*P(L=1|G=3)*P(S=1|I=1)

=0.6*0.3*P(G=3|I=1,D=0)*P(L=1|G=3)*P(S=1|I=1)

=0.6*0.3*0.7*0.01*0.8

此外，在实际应用过程中，还将出现求两个联合概率分布乘积的情况。依旧以离散概率分布为例：

上图给出了两个联合概率分布的运算法则：

P(A,B,C)=P(A,B)*P(B,C)

三 贝叶斯网络的定义

通过前面的介绍，我们已经知道，Factor是组成PGM模型的基本元素，概率分布通过Factor之前的关系传递。接下来，我们先给出贝叶斯的网的定义，然后再来体会由Factor构成PGM模型的过程 。

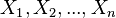贝叶斯网络(Bayesian network)，又称有向无环图模型(directed acyclic graphical model)，是一种概率图型模型，借由有向无环图(directed acyclic graphs, or DAGs )中得知一组随机变量{}及其n组条件概率分配(conditional probability distributions, or CPDs)的性质。举例而言，贝叶斯网络可用来表示疾病和其相关症状间的概率关系；倘若已知某种症状下，贝叶斯网络就可用来计算各种可能罹患疾病之发生概率。

一般而言，贝叶斯网络的有向无环图中的节点表示随机变量，它们可以是可观察到的变量，抑或是隐变量、未知参数等。连接两个节点的箭头代表此两个随机变量是具有因果关系或是非条件独立的；而节点中变量间若没有箭头相互连接一起的情况就称其随机变量彼此间为条件独立。若两个节点间以一个单箭头连接在一起，表示其中一个节点是“因(parents)”，另一个是“果(descendants or children)”，两节点就会产生一个条件概率值。

令G = (I,E)表示一个有向无环图(DAG)，其中I代表图形中所有的节点的集合，而E代表有向连接线段的集合，且令X = (X_i)_i ∈ I为其有向无环图中的某一节点i所代表之随机变量，若节点X的联合概率分配可以表示成:

则称X为相对于一有向无环图G 的贝叶斯网络，其中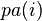表示节点i之“因”。

对任意的随机变量，其联合分配可由各自的局部条件概率分配相乘而得出：

       

依照上式，我们可以将一贝叶斯网络的联合概率分配写成：

       ,  对每个相对于X_i的“因”变量X_j 而言)

 

    上面两个表示式之差别在于条件概率的部分，在贝叶斯网络中，若已知其“因”变量下，某些节点会与其“因”变量条件独立，只有与“因”变量有关的节点才会有条件概率的存在。这就是后面我们要重点理解的，影响因子的推理规则。