[洛谷 P4612][COCI 2011-2012#7] Setnja

传送门

TM :setnja (1S256M)

一个人要散步去会见他的 N 个朋友（按给定的顺序会见）。我们可以理解成他们都住在一个

很大的网格内，每个朋友住其中的一个单元格，所有人每一步都可以走到相邻的八个格子中。
每个朋友最多可以走 P 步与他相见，每个人的 P 值不一定相同。他可以决定起点和终点。
问他会见完所有朋友的最少步数。
输入：
第一行，一个正整数 N (2 ≤ N ≤ 200 000)，表示朋友个数。
接下来，N 行，描述 N 个朋友，x, y, and P (0 ≤ x, y, P ≤ 200 000)，x,y 表示朋友最初的坐
标。朋友给的顺序就是他要依次会见的顺序。
输出：
一个数，表示他要走的最少的步数。
Scoring
30%的数据，所有数字最多 20.
另有 30%的数据，所有朋友的 P 值小于 10.
样例：
Input
3
3 10 2
8 4 2
2 5 2
output
4
input
4
3 3 5
7 11 5
20 8 10
30 18 3
output
19
样例 1，从 (4, 8),出发会见第一个朋友。走两步在（6，6）会见第二个朋友，走两步到（4，5）会见第三个朋友。

代码 ：

#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;

;
;
struct size_ {
    int x1, x2, y1, y2;
    size_ () {}
    size_ (int x1, int x2, int y1, int y2) : x1(x1), x2(x2), y1(y1), y2(y2) {}
}c[N];

size_ cmp(size_ a, size_ b) {
    size_ w(max(a.x1, b.x1), min(a.x2, b.x2), max(a.y1, b.y1), min(a.y2, b.y2));
    if( w.x1 > w.x2 || w.y1 > w.y2) return size_ (-inf, -inf, -inf, -inf);
    return w;
}

int n;
int main() {
    freopen("setnja.in", "r", stdin);
    freopen("setnja.out", "w", stdout);
    scanf("%d", &n);
    , x, y, p; i <= n; i ++)
        scanf("%d%d%d", &x, &y, &p), c[i] = size_(x-p, x+p, y-p, y+p);
    size_ w = c[];
        long long ans = 0ll; // 开 long long ，不然会炸
    ; i <= n; i ++) {
        size_ t = cmp(w, c[i]);
        if( t.x1 != -inf) {    w = t; continue ;}
        int x = max(max(w.x1 - c[i].x2, c[i].x1 - w.x2), max(w.y1 - c[i].y2, c[i].y1 - w.y2));
//        printf("%d %d<< \n", x, i); // de bug
        w = cmp(size_(w.x1-x, w.x2+x, w.y1-x, w.y2+x), c[i]); ans += (long long)x;
    }
    printf("%lld", ans);
    ;
}   

时间较短，博主考试炸了要改题，为什么这么做后2天找时间补上

开始填坑......

　　惯例 设 struct---- C[  ] { x1, x2(横坐标  x1 < x2), y1, y2(纵坐标 y1  <  y2) } ( 表示那个 基♂友最多愿意活动的范围）

　　因为他必须按顺序访问节点，所以贪心去找就 ojbk......

首先

　　我们考虑样例1(我觉得结合样例更容易说清)

　　

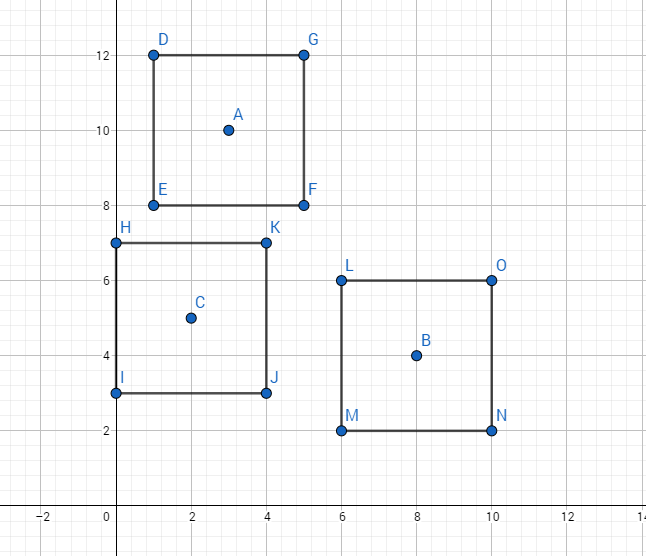
　　图中 A B C 表示 这位死宅的基♂友的初始位置， 周围的矩形表示他的基♂友愿意活动的范围......

　　因为我们可以选定初始位置，所以起点应该在A矩形内的任意位置(当前), 如果在矩形外的话一定不是最优解(很容易YY到),那么从A矩形到B矩形的最短距离便是从A访问B的最短距离

　　可以看到，最短距离便是FP，(因为可以斜着走，FQ不够长，到不了);

　　今天先填到这......

---

前面在说什么不太记得清了，能看就看，重新整理下

　　每个人能到达的范围可以用一个矩形来表示(显然), 第一次的位置一定是在第一个人活动的区域(如果在区域外那么他将先走到区域内在走到第二个人那里去，显然不是最优);

然后(1 ) 如果第二个点的范围与第一个点有交集，那么初始可行位置一定是在这个交集里面(YY下就好了);

　　(2 ) 如果第二个点的范围与第一个点无交集，那么需要移动的距离一定是第一个矩形与第二个矩形之间的最短距离，那么将第一个矩形扩大最短距离个单位，与第二个矩形的交集便是最优解可能的位置，此时 ans 加上之前求出的最短距离。

然后我们得出的最优解的范围与之后的点进行同样的操作，贪心即可得出最优解......

至于为什么......看图......

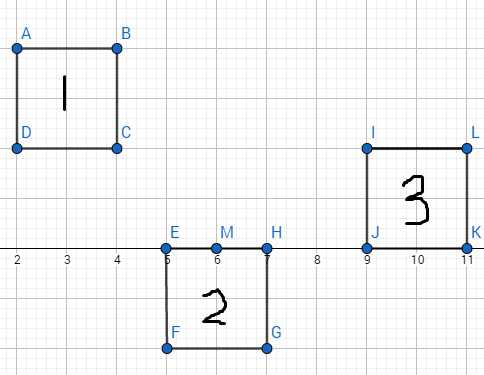
第一次我们得出1与2的最短距离是2，则最优范围从ABCD变道EM，然后再由EM去扩展得到2与3 的最优范围。(还不理解就自己画画图);

然后历时2天的坑就填完了......

---