.Net程序员 Solr-5.3之旅 (二)Solr 安装

阅读目录

• 引言
• Solr5.3环境搭建
• Solr5.3创建第一个Core
• 结尾

引言

一个糟糕的设计有好的表现形式，它会被判死缓，一个好的设计有糟糕的表现形式，它会被判死刑立即执行。

以上摘自一个设计师的话，于原句可能有些出入，但是精髓都是一样。每个人有都有的自己的理解，我的理解是——了解你的客户的需求，了解他们需要什么，用任何技术手段达到它。

回到顶部

Solr5.3环境搭建

废话不多说，今天直接进入我们的主题，前面介绍了Solr的前世今生，今天我们就开始正式来玩一玩。

1.下载Solr5.3.1

solr-5.3.1-src.tgz(源代码)如果你想后期直接修改源代码重新编译发布属于自己的特殊版本可以下载，.Net程序员可以跳过

solr-5.3.1.zip(Solr编译好的版本)，PS:编译好的文件里面含有文档，所以反而大了很多。

2. 解压.....

3. 将 solr 压缩包中 solr-5.3.0\server\lib\ext 中的 jar 全部复制到 Tomcat\ webapps\solr\WEB-INF\lib 目录中,Tomcat是啥，不会忘记了吧，上篇我们已经安装好Tomcat环境。

4. 将 solr 压缩包中 solr-5.3.0/ server/resources /log4j.properties 复制到Tomcat\ webapps\solr\WEB-INF\lib 目录中

5. 将 solr 压缩包中 solr-5.3.0/server/solr 目录复制到计算机某个目录下，如D:\solr_home

5.打开Tomcat/webapps/solr/WEB-INF下的web.xml，找到如下配置内容（初始状态下该内容是被注释掉的）：

    <env-entry>
    <env-entry-name>solr/home</env-entry-name>
    <env-entry-value>D:\solr_home</env-entry-value>
    <env-entry-type>java.lang.String</env-entry-type>
    </env-entry>

其中D:\solr_home为我们刚才第5点创建的文件夹路径

6.保存关闭，而后启动tomcat，在浏览器输入http://localhost:9080/solr即可出现Solr的管理界面,我这里配置的端口是9080

回到顶部

Solr5.3创建第一个Core

solr-5.3.1\example\example-DIH\solr\solr 这个目录里面放的是例子，我这里采用直接从数据库导入数据到Core中

1.在D:\solr_home下新建一个文件夹，名字可以是你的表名，我这里用FixValue

2.将solr-5.3.1\example\example-DIH\solr\solr下的文件拷贝到你所新建的文件夹里面，D:\solr_home\FixValue

3.启动Solr，或者点击ReStart

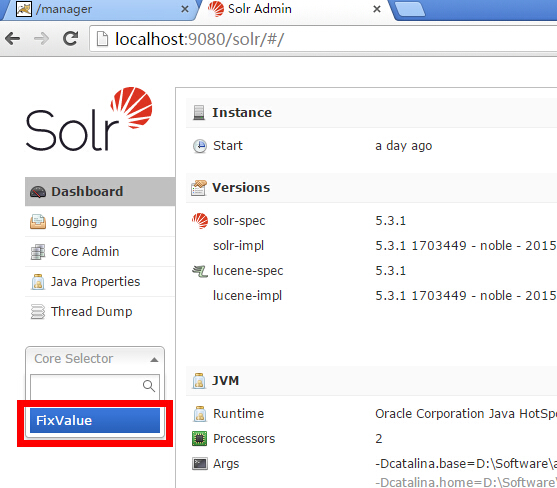
analysis分析，在这里可以选择某个字段，然后输入文本，测试你的数据导入到Solr后分词情况。后面文章会讲到如何配置自己的分词解析器

dataimport数据导入，后面将数据库数据导入到solr需要用到这个功能

documents文档，在这里可以对Solr中的索引文件进行增、删、改（我也还没用过这个功能）

Query查询，这里可以对已经存在Solr中的文档进行查询，这个功能页面是我们后面开发其他查询主要使用到的工具页面

回到顶部

结尾

下一篇我们讲述，如何使用Solr从MSSQ将索引导入索引（数据）

回到顶部