支持向量机SVM知识梳理和在sklearn库中的应用

SVM发展史

线性SVM=线性分类器+最大间隔

间隔(margin):边界的活动范围。The margin of a linear classifier is defined as the width that the boundary could be increased by before hitting a data point.

预备知识

• 线性分类器的分割平面(超平面)：Wx+b=0
• 点到超平面的距离:\(M=\frac{ \vert g(x) \vert }{\left\|W\right\| }\),其中\(g(x)=Wx+b\)
• SVM中正样本定义为g(x)>=1,负样本定义为g(x)<=-1
• SVM中Wx+b=1或者Wx+b=-1的点称为支持向量

间隔的形式化描述

\(M=\frac{2}{\left\|W\right\| }\)

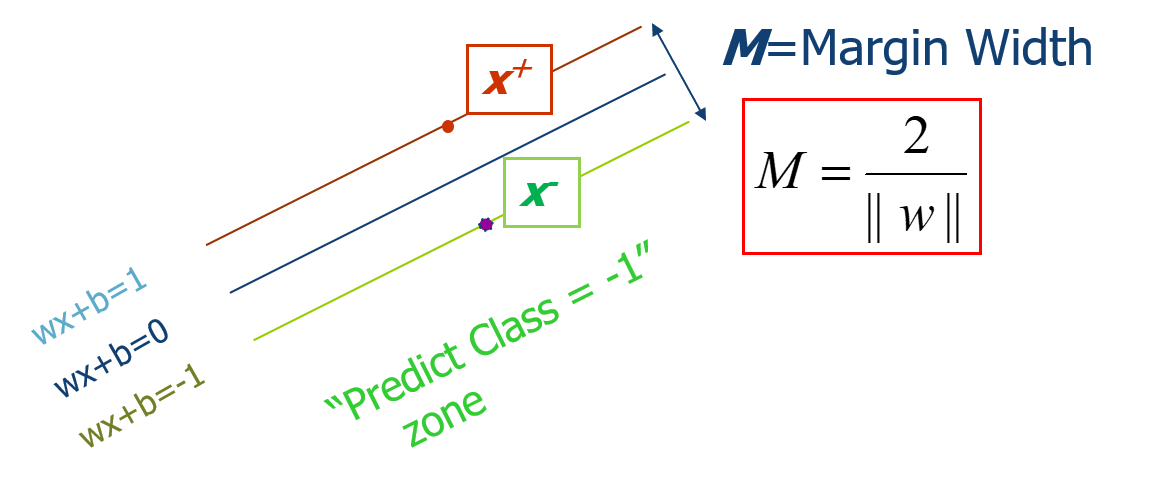
SVM通过最大化M来求解参数W和b的，目标函数如下：

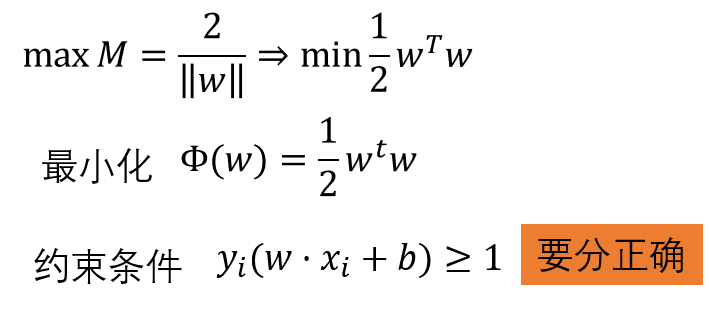
求解 ：拉格朗日乘数法，偏导为0后回带

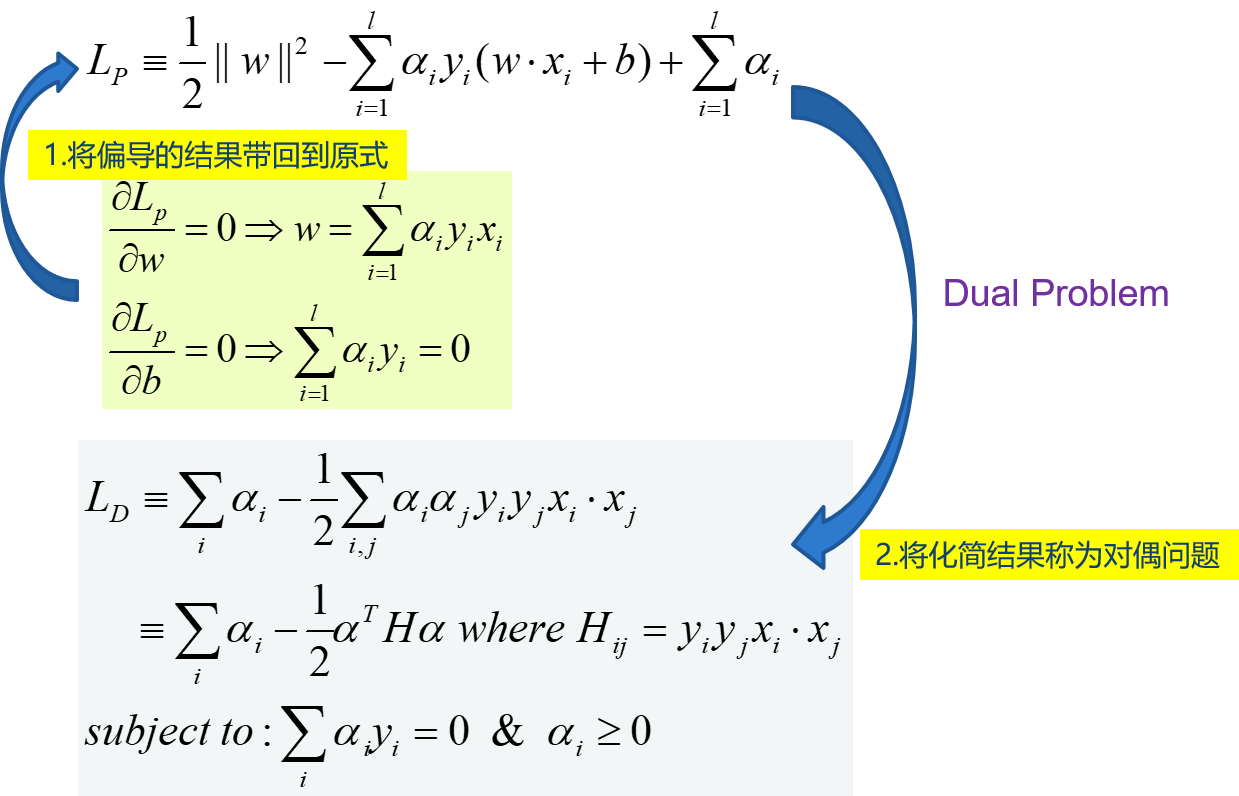
在SVM中，原问题和对偶问题具有相同的解，W已经求出：\(W=\sum_{i=1}^{l}{\alpha_iy_ix_i}\), 不等式约束，还需要满足KKT条件。若\(\alpha_i>0\),则必有xi为支持向量，即：训练完毕后，最终模型仅和支持向量有关。

b的求解过程如下

一个实例

软间隔：加入容错量

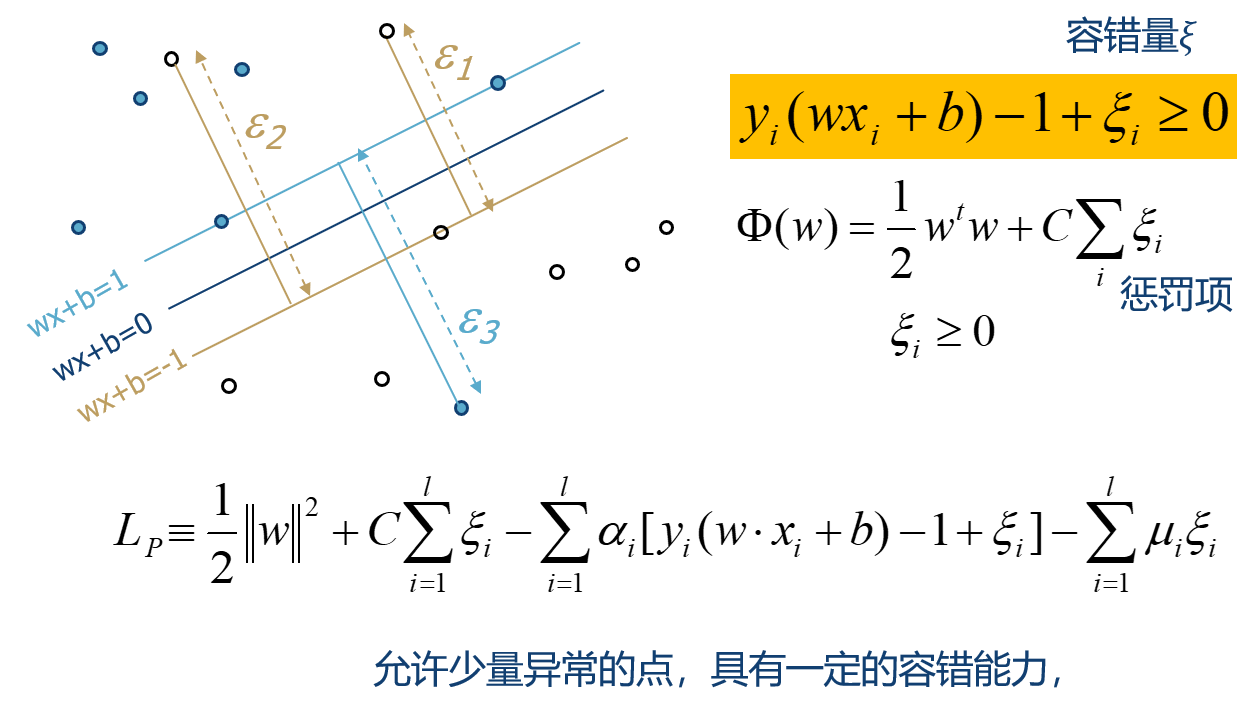
同样采用拉格朗日乘数法求解

LD的区别仅仅体现为\(\alpha_i\)的约束不同。

非线性SVM:特征空间

通过映射到高维空间来将线性不可分的问题转换为线性可分的问题。

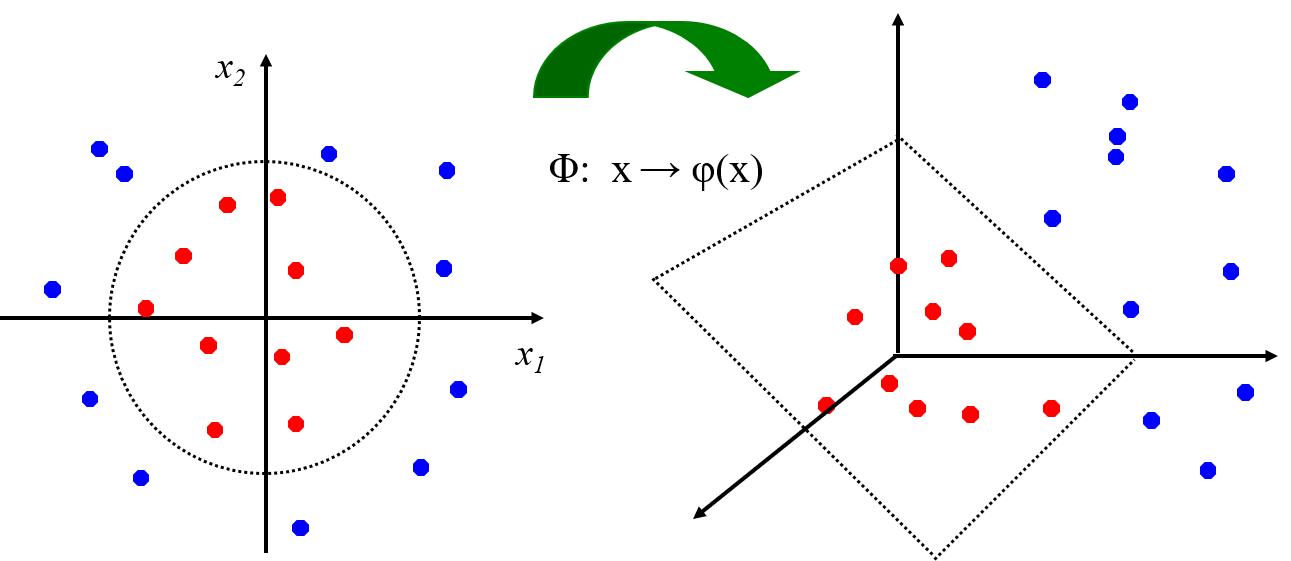
高维空间向量内积运算复杂度高。以二次型为例，直接计算

\(x_i⋅x_j⇒Φ(x_i)⋅Φ(x_j)\),直接计算的话，复杂度会成倍增加。

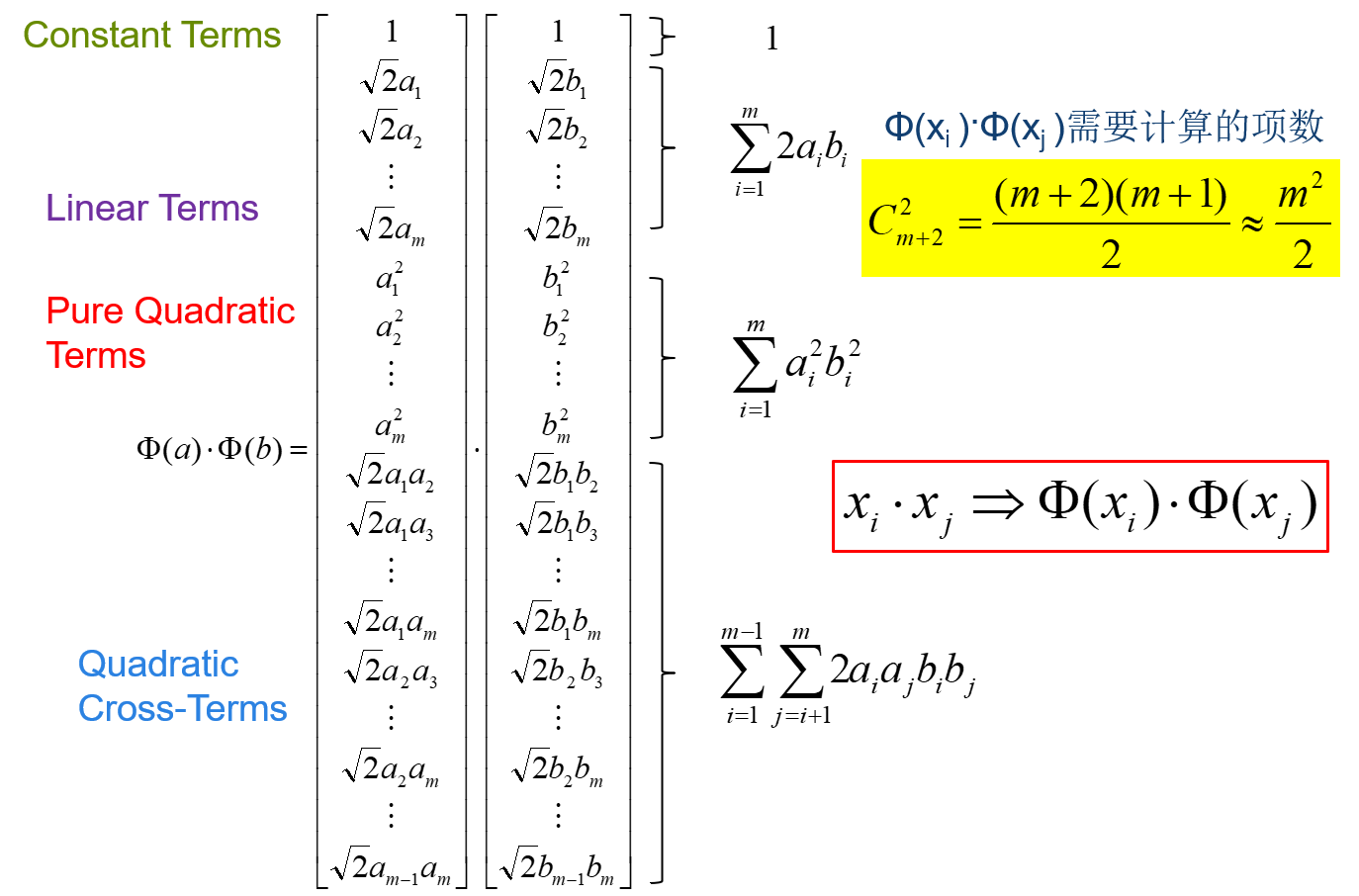
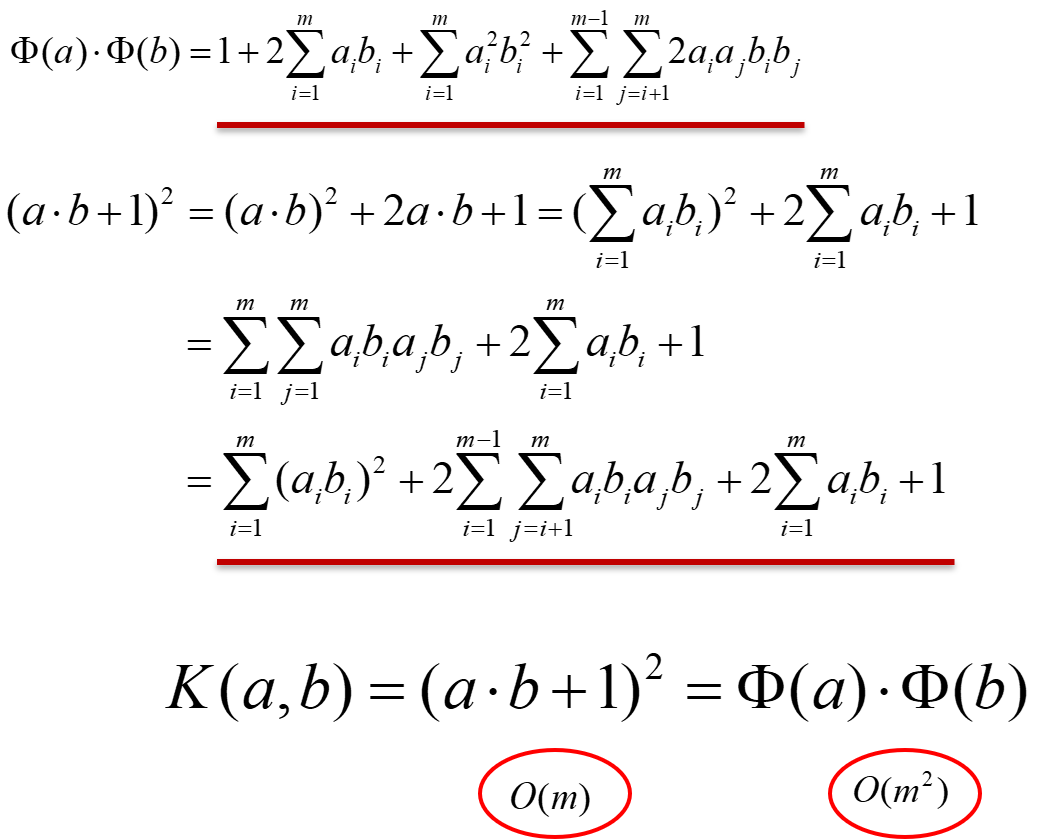
以二次型为例，理解核技巧

通过在低维空间的计算o(m)，得到高维空间的结果，不需要知道变换是什么，更不需要变换结果的内积，只需要知道核函数，就可以达到相同的目标。(变换结果的内积)

请看实例,二维空间

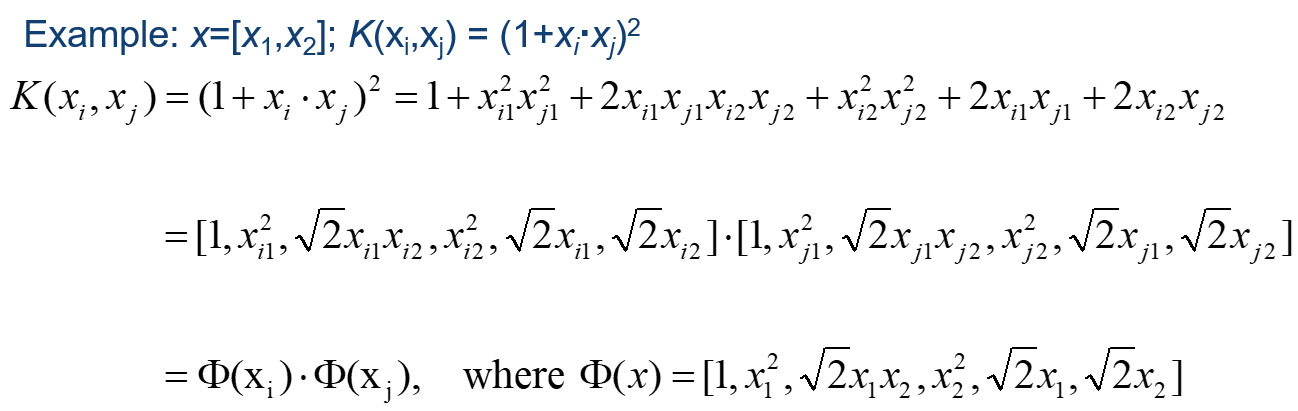
常用的核函数

多项式变换中，当d=2时，就是二次型变换。

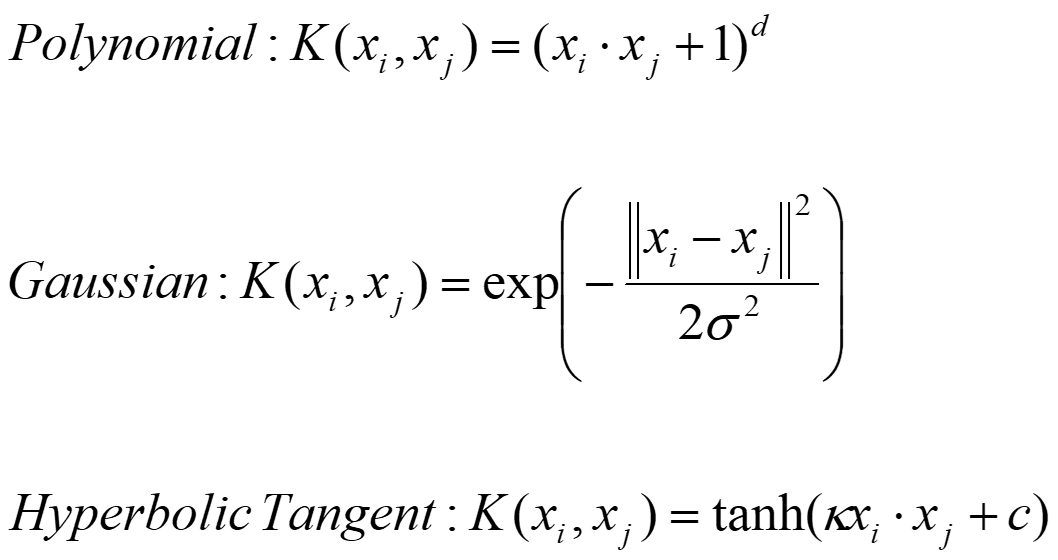
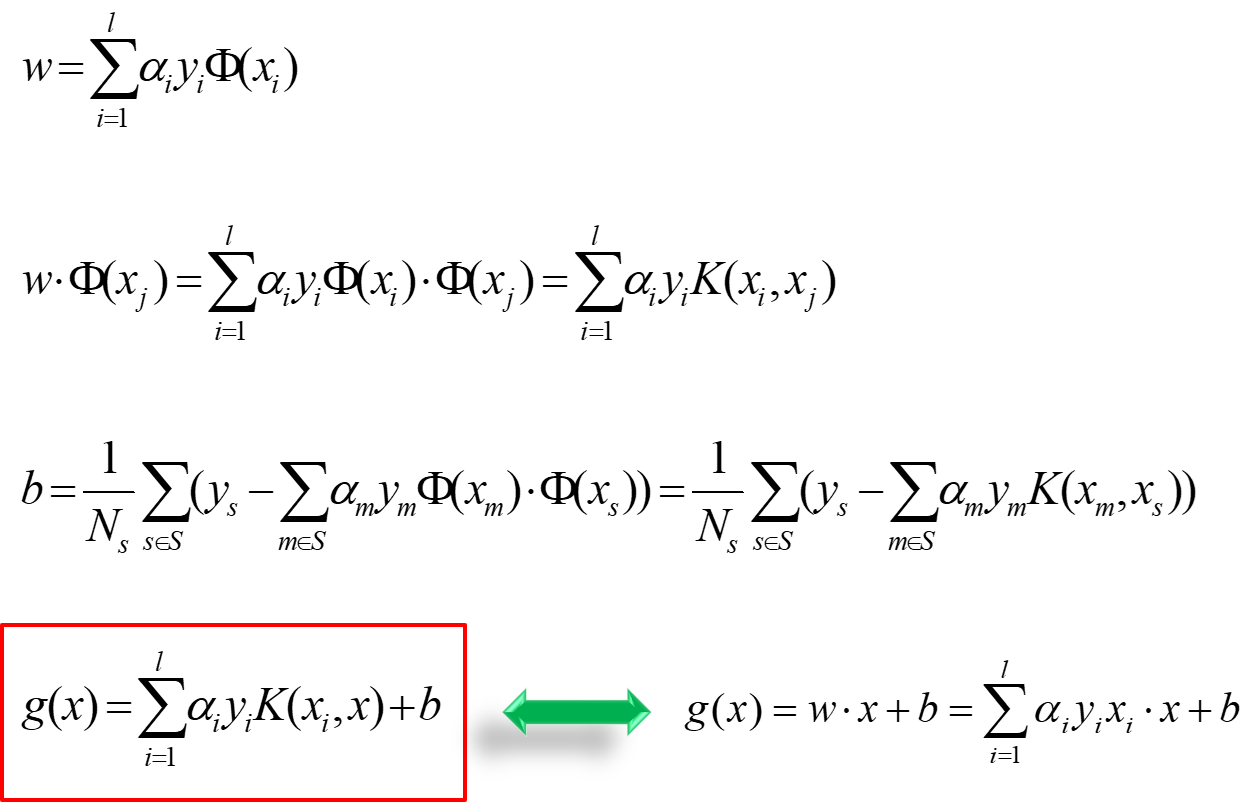
此时w和b的结果如下：

将\(x_i\)换为\(\phi(x_i)\),将\(\phi(x_i)\cdot \phi(x_j)\)换为\(K(x_i,x_j)\),其余都不变，真的很简洁。

SVM在Scikit-Learn中的应用

• Linear SVM:\(min\frac{1}{2}\left\|w\right\|^2+C\sum{\zeta^2}\)

LinearSVC(
    penalty='l2',
    C=1.0,#就是目标函数的C，C越大(eg:1e9)，容错空间越小，越接近硬边界的SVM(最初的SVM，基本不用),C越小(eg:C=0.01)，容错空间越大，越接近soft Magin.
)

• 核函数 SVM:from sklearn.svm import SVC

SVC(
    C=1.0,
    kernel='rbf',
    degree=3,#多项式核函数的指数d
    gamma='scale',#高斯基函数中的参数gamma，越大，函数分布越狭窄； gamma越小，决策边界越松弛，当很小时，可以认为趋于无穷大成一条直线了，这时就欠拟合了。gamma取值越大，决策边界越收紧，当很小时，会无限包紧样本点，这时就过拟合了。
)