日日算法：Dijkstra算法

介绍

Dijistra算法作为一种最短路径算法，可以用来计算一个节点到图上其他节点的最短距离。

主要是通过启发式的思想，由中心节点层层向外拓展，直到找到中点。

适用于无向图和有向图。

算法思想

1. 假设我们要计算节点A到其它节点的最短距离
2. 引入两个集合（S，U），其中集合S表示已经求出最短路径的点（以及最短距离），集合U表示还未求出最短路径的点。集合中的元素用类似A(0)形式表示，其中A目标点为A，(0)表示目前已知最短路径为0（未直接连通的距离用∞表示）。
3. 初始时，S集合中只有起始点，距离为0，U集合中除了直接与A点连通的点外，距离都为∞。
4. 第一次向外拓展，找出U集合中距离最短的点（假设为B）加入集合S。并以B点向外拓展，更新U集合中的距离值。更新规则为，如果经过B到某点的距离小于U集合中记录的结果，那么则更新中集合U中该点的距离值。
5. 每执行一次步骤四，我们可以得出A点距某个点的最短距离。
6. 重复步骤四，直到U的集合为空或是目标点不在U集合中，也就计算出了需要的最短距离。

用图表示解题过程:

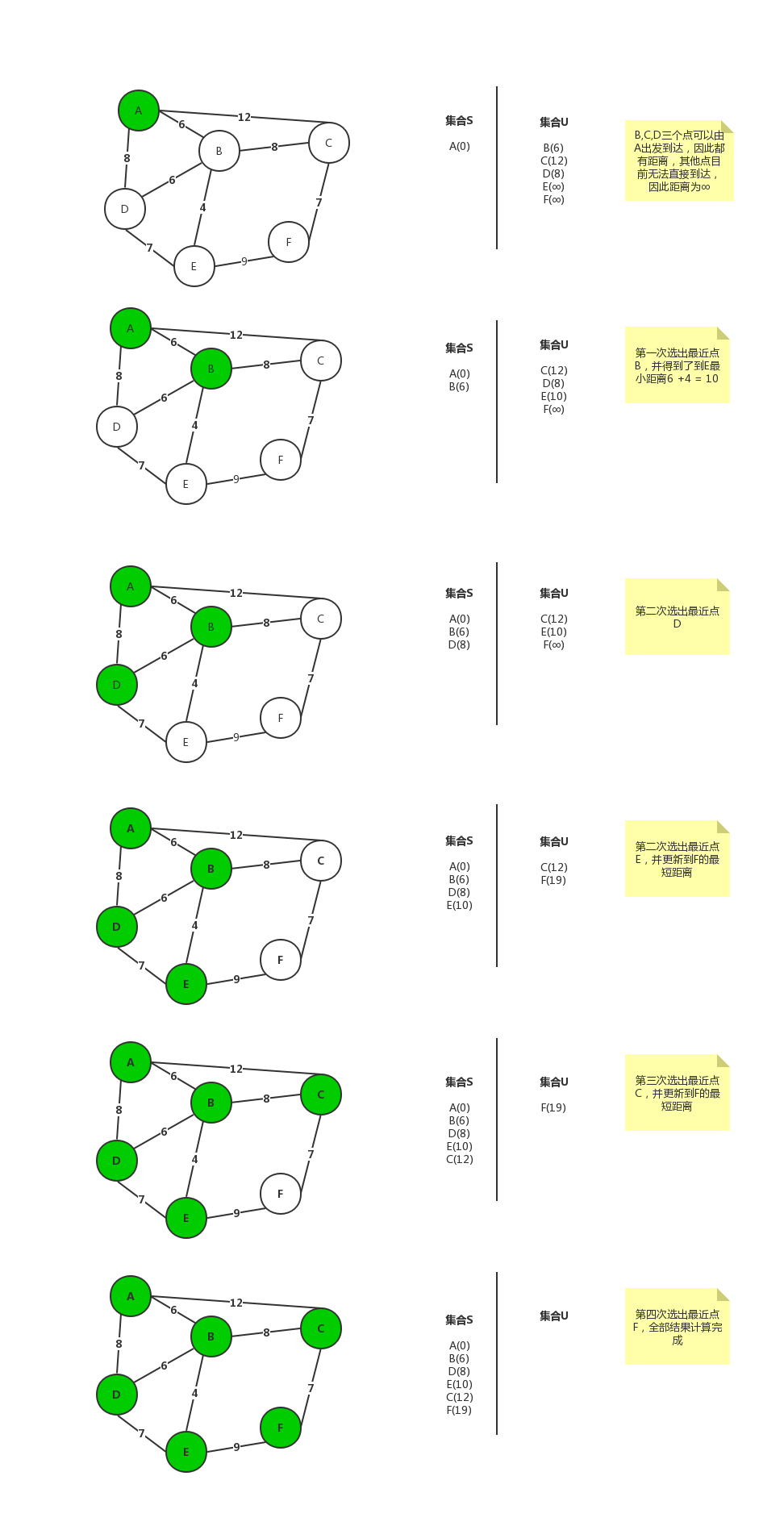
证明

同样以上图为例，我们如何保证第一次选择得到结果A-> B (6)是正确的最优解。

证明：

• 上述图为无向图，且不存在负权边。
• 由A出发去其他点，穷举第一条边所有选择，只能为A -> B（6），A -> C（12） 和 A -> D（8）三种。一旦第一条边选择了后两种情况，经过C或是D点再绕回B，由于不存在负权边，那么经过C的路线一定大于A->C(12)，经过D的路线A->D(8)，因此都会大于A ->B(6)。
• 那么为什么第二次选择只能确定D而非刚更新了最小值的E点。首先基于上一步我们确定了由A出发去D点最短路径第一条边只可能是A->B和A->D两种情况，而经过B点再选择第二条边也在上轮计算过了，其与第一条边之和均大于A->D(8)，所以能够确定到D的最短路径。而由于D->E的最短路径在第二轮尚不知道，因此无法确定到E的最短路径。
• 同理，可以确定每一轮的解都是最短路径。

算法实现

public class Dijkstra {
    public static int[] getShortestPath(int[][] graph, int source){
        if(graph == null || graph.length <= source)
            throw new IllegalArgumentException();
        if(graph.length != graph[0].length)
            throw new IllegalArgumentException();
        int n = graph[source].length;
//        String[] route = new String[n];
        //保存结果集
        int[] ret = new int[graph[source].length];
        //保存已确定最短路径的点
        int[] visited = new int[graph[source].length];
        //初始化数据
        Arrays.fill(visited, 0);
        Arrays.fill(ret, Integer.MAX_VALUE);
        ret[source] = 0;
        //进行n次筛选
        for(int i=0; i<n; i++){
            //找出结果集中未visited结果中数据最小的点，为该轮确定的最短路径
            int minValueIndex = findMinValue(ret, visited);
            visited[minValueIndex] = 1;
            //更新通过该点是否有新的最短路径生成
            int[] line = graph[minValueIndex];
            for(int j=0; j<line.length; j++){
                if(visited[j] == 0 &&
                        line[j] != Integer.MAX_VALUE &&
                        line[j] + ret[minValueIndex] <= ret[j]){
                    ret[j] = line[j] + ret[minValueIndex];
                }
            }
        }
        return ret;
    }
    private static int findMinValue(int[] source, int[] visited){
        int ret = 0;
        int minVal = Integer.MAX_VALUE;
        for(int i=0; i<source.length; i++){
            if(visited[i] == 0 && source[i] < minVal){
                ret = i;
                minVal = source[i];
            }
        }
        return ret;
    }
}

上述代码见Github。