NOI ONLINE 入门组魔法矩阵快速幂

做了这道题我才发现NOI入门组!=NOIP普及组

题目链接

　　https://www.luogu.com.cn/problem/P6190

题意

　　给出一张有向图，你有K次机会可以反转一条边的边权，即让它变成自己的相反数，但只有一次有效，也就是说当你走过这条边后，这条边的边权就会又变回去，如果没有这个性质，那么在出现环时，就可以无限刷边权了。

分析

　　看到这道题的时候，我第一想到的，这不就是分层图最短路嘛，应该还是个板子，看到数据的时候我惊了，K<=10⁶，这好像也没办法开数组吧，但由于我技术有限，所以当时就只打了一个分层图最短路，在洛谷上评测的时候，理论上是可以拿到90分的，除了最后两个点不过，但我只有85分，有一个点一直不能A，不知道为什么。

　　后来的时候也没怎么想这道题，我以为有更牛13的方法可以开下这个数组，直到前几天看见有人说这题用矩阵做？我当时就对这道题产生了好奇心，矩阵怎么做。。。后来看了看题解，自己又简单分析了一下，大概是掌握了，首先我们先来分析数据，K的值很大而n却很小，当时我一直没有注意到这一点，这可以启示我们什么？我们可以通过状态的递推来使得K不断减小，而n又这么小，n³的效率也可以接受，所以考虑使用floyd算法，因为刚接触最短路算法没几个月，可能觉得floyd算法的实用性不是很高，因为有的时候n给的范围连数组都开不下，所以我们一般都会用dij或是spfa来跑最短路，但很关键的一点是什么，不管是dij还是spfa都是单源最短路，也就是说起点是确定的，而floyd算法，虽然n³但可以一次性跑出每个点之间的最短路，并且它还是一个矩阵，floyd算法的公式大家应该都会写，写出来如果把min换成+后，再观察一下，是不是和矩阵乘法十分像？那是不是同样可以考虑使用矩阵快速幂优化？所以可以考虑从这个地方下手。

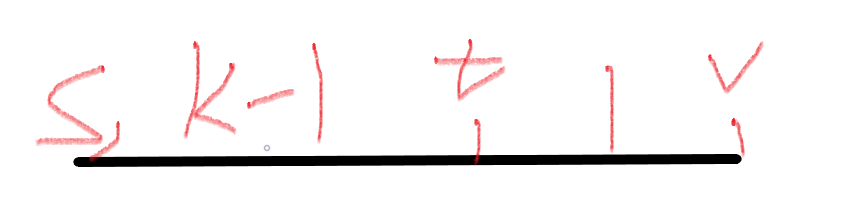
　　先来考虑带着K进行转移，假设F[k][i][j]表示从i到j至多用了k次魔法的最短路径，为什么是至多而不是恰好呢?假如A->B就只有两条有向边，走过去就走不回来了，那么F[10][A][B]==F[2][A][B]是显然的，那么如果我们定义为恰好，那么就会导致F[10][A][B]求不出来，所以在转移的时候就会出现问题。接着考虑F[k][i][j]，看下图，我们假设从s到t至多用了k-1次魔法，从t到v至多用了1次魔法，那么

　　　　　　　　　　　　　　　　　　　　　　F[k][s][v]=min(F[k][s][v],F[k-1][s][t]+F[1][t][v])

是显然可以看出的，如果我们对任意s，v，枚举t，是不是就可以得出s，v之间的最短路了呢？这也是显然的吧。这里就体现出了floyd的好处了，这是dij和spfa所不能拥有的，就是任意两点之间的最短路都可以求出，在这一点上dij和spfa是赶不上的floyd的，那么我们就已经接近正确答案了，毕竟递推公式都有了，是吧。

　　但是这个递推公式解决的问题其实不多，在不要求时间的情况下是可以解决这个问题的，但这是竞赛啊，时间卡的很死，所以考虑进行优化，观察上述递推式，是不是很熟悉？min改成+后再看看，这不就又是矩阵乘法了嘛？所以我们可以定义一种矩阵运算，让矩阵A*B为矩阵乘法的加号改成min后运算得到的结果，这个时候，令矩阵F[k]表示至多使用k次魔法后，每个点之间的最短路，由上述递推式可以得到

　　　　　　　　　　　　　　　　　　　　　　　　　 F[k]=F[k-1]F[1]　(为重定义后的运算符)

　　那么F[k-1]呢，F[k-1]=F[k-2]*F[1]对吧，这里不难推出，F[k]=k个F[1]运算，接下来我们只要考虑这个运算能不能使用结合律，如果可以，那完全可以用快速幂优化，而取min的话，不管怎么取，最小值都是不会变的，所以这个运算是可以使用结合律的，那么我们也可以用矩阵快速幂优化。

　　所以上述递推式又变成了F[k]=F[1]^k,我们只要求出F[1]即可，F[1]表示的是啥？至多使用一次魔法的最短路呗，所以F[1]可以由F[0]即floyd数组转移过来，枚举每条边即可。

　　分析到这里，代码基本上就已经出来了，写起来很简单，但思路很不好想，这道题让我知道了可以从数据范围来考虑解法，因为题目是一定有解的嘛，所以给出的数据范围大小一定有它的道理的，从这方面下手有时候也许也不错。

 #include<cstdio>

 #include<algorithm>

 #include<cstring>

 #include<cmath>

 #define ll long long

 using namespace std;

 const int N=+;

 ll dis[N][N],f[N][N];

 struct Edge{

     ll from,to,val;

 }e[*N];//因为要枚举边所以要开一个结构体

 ll m,n,k;

 void Ins(ll a,ll b,ll c,ll len){

     e[len].to=b;e[len].val=c;e[len].from=a;

 }

 void Mul(ll d[N][N],ll a[N][N],ll b[N][N]){

     ll t[N][N];

     memset(t,0x3f,sizeof(t));

     for(ll i=;i<=n;i++)

         for(ll j=;j<=n;j++)

             for(ll k=;k<=n;k++)

                 t[i][j]=min(t[i][j],a[i][k]+b[k][j]);//重定义后的矩阵运算

     memcpy(d,t,sizeof(t));

 }

 int main(){

     scanf("%lld%lld%lld",&n,&m,&k);

     memset(dis,0x3f,sizeof(dis));

     for(ll i=;i<=n;i++)//最开始除了到自己外全为正无穷

         dis[i][i]=;

     for(ll i=;i<=m;i++){

         ll a,b,c;

         scanf("%lld%lld%lld",&a,&b,&c);

         Ins(a,b,c,i);

         dis[a][b]=c;//无重边自环直接赋值就行

     }

     for(ll cc=;cc<=n;cc++){

         for(ll i=;i<=n;i++){

             for(ll j=;j<=n;j++){

                 dis[i][j]=min(dis[i][j],dis[i][cc]+dis[cc][j]);//floyd

             }

         }

     }

     memcpy(f,dis,sizeof(dis));

     for(ll i=;i<=m;i++){

         ll u=e[i].from,v=e[i].to,w=e[i].val;

         for(ll j=;j<=n;j++)

             for(ll cc=;cc<=n;cc++)

                 f[j][cc]=min(f[j][cc],dis[j][u]-w+dis[v][cc]);//F[1]

     }

     for(;k;k>>=){//矩阵快速幂

         if(k&)Mul(dis,dis,f);

         Mul(f,f,f);

     }

     printf("%lld\n",dis[][n]);

     return ;

 }